Tensor Logic: One Equation to Rule Them All

Machine learning and symbolic AI have been fighting for sixty years. Pedro Domingos thinks they're the same thing.

His recent paper proposes something audacious: "Tensor Logic is a programming language with an underlying theory that unifies neural and symbolic approaches to AI, using the fact that a logical rule can be equivalently written as a tensor equation in Einstein summation notation."¹ If he's right, we've been building separate tools for problems that share identical mathematical structure.

The claim isn't that neural networks and logic systems can be made to work together. Plenty of researchers have tried that.² The claim is that they're literally the same operation written in different notation. A logical rule with universally quantified variables corresponds exactly to a tensor equation where types map to embedding dimensions, constants to embeddings, predicates to tensors, functions to mappings between types, and variables to tensor indices.³

This isn't incremental progress. It's a statement that the field has been solving one problem with incompatible dialects.

The Fragmentation Problem

Anyone building AI systems today knows the pain. You want a model that can learn from data? PyTorch. You want formal reasoning with guarantees? Prolog or a theorem prover. You want probabilistic inference? Stan or a graphical model library. You want all three? Good luck wiring them together.

The neuro-symbolic AI community has been trying to bridge this gap for years. A recent systematic review analyzed 167 papers on the topic, finding that "the majority of research efforts are concentrated in the areas of learning and inference (63%), logic and reasoning (35%), and knowledge representation (44%)."⁴ That's a lot of effort spent building bridges between things that shouldn't need bridges.

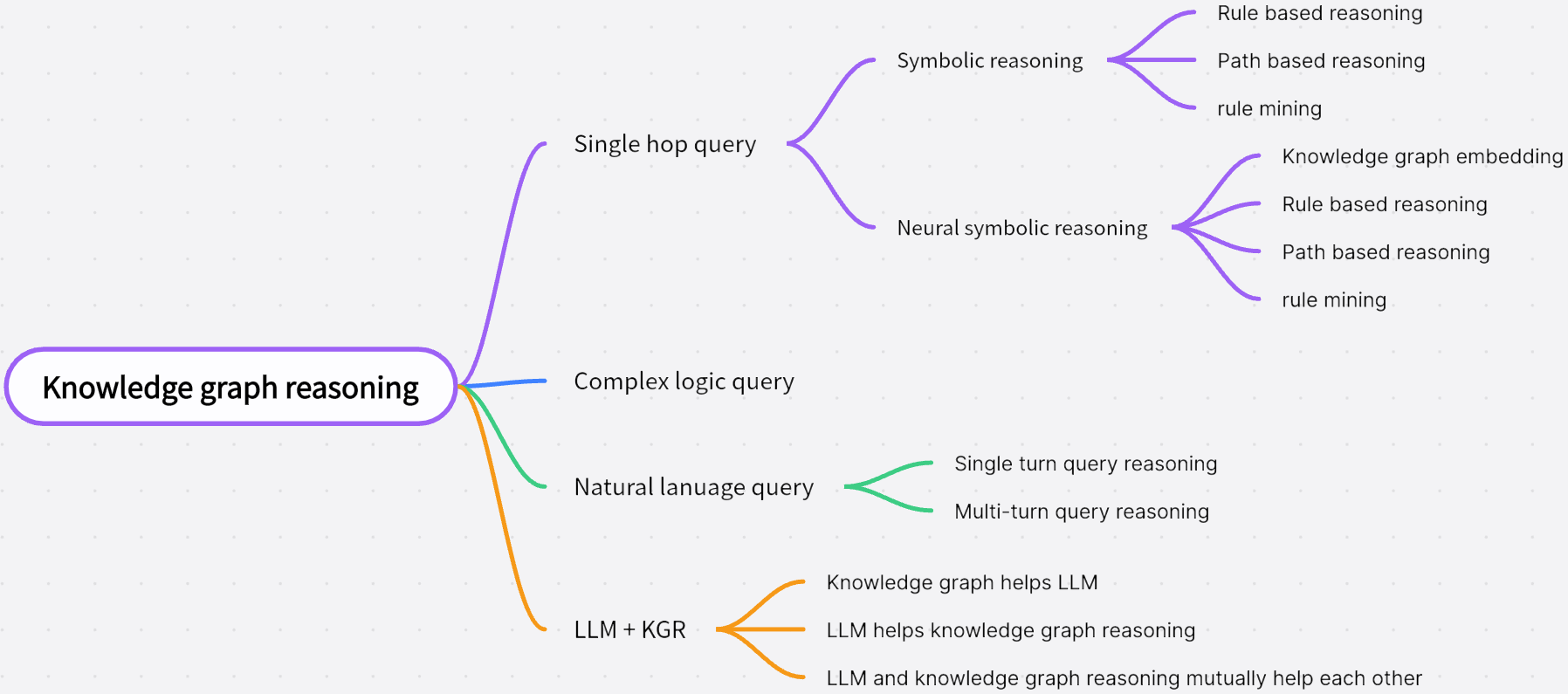Figure 1: The taxonomy of neuro-symbolic approaches shows how researchers have been combining symbolic reasoning with neural learning through various hybrid methods. Source: Neural-Symbolic KG Reasoning Survey (arXiv:2412.10390), Figure 1

The field has produced impressive hybrid systems. AlphaGeometry sits at the intersection of explainability, knowledge representation, learning and inference, and logic and reasoning.⁵ DeepProbLog "combines domain knowledge specified as Prolog rules with neural network outputs, handling uncertainty through probabilistic reasoning."⁶ Logic Tensor Networks integrate first-order logic constraints into neural network training.⁷

But these are integration frameworks, not unifications. They're sophisticated plumbing connecting distinct computational systems. Every one requires the developer to think in multiple languages and manage the translation overhead.

The Correspondence: Logic as Tensor Equations

Here's where Domingos makes his move. He observes that Einstein summation notation and logical inference perform structurally identical operations.

Consider a logical rule:

grandparent(X, Z) :- parent(X, Y), parent(Y, Z).

This says: X is a grandparent of Z if there exists some Y such that X is a parent of Y and Y is a parent of Z.

Now represent the parent relation as a tensor $P_{xy}$ where $P_{xy} = 1$ if person $x$ is a parent of person $y$, and 0 otherwise. The grandparent relation becomes:

$G_{xz} = P_{xy} P_{yz}$

The repeated index $y$ is summed over. If any intermediate person $y$ connects $x$ to $z$ through two parent relations, the result is nonzero. This is Einstein summation: repeated indices imply summation.

The correspondence extends systematically:

• Types map to embedding dimensions: If people are represented as 512-dimensional vectors, the index ranges over 512.
• Constants map to specific embeddings: "Alice" becomes a particular 512-dimensional vector.
• Predicates map to tensors: The parent relation becomes a matrix (2-tensor).
• Variables map to tensor indices: $X$, $Y$, $Z$ become indices $x$, $y$, $z$.
• Logical conjunction maps to tensor product: AND becomes multiplication.
• Existential quantification maps to contraction: "there exists Y" becomes summation over $y$.

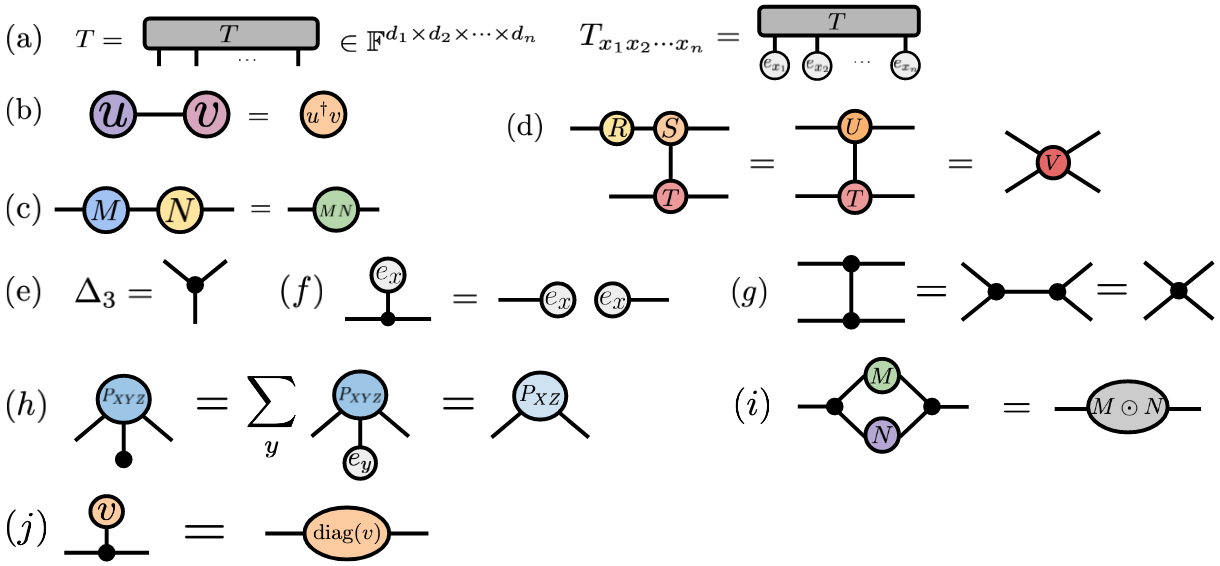Figure 2: Tensor network diagrams provide a visual calculus for tensor operations. Nodes represent tensors, edges represent indices, and connected edges indicate contraction (summation). Source: PGM and Tensor Networks (arXiv:2106.15666), Figure 1

"TensorLog aims to find answers for a given query by matrix multiplication. The idea of Tensorlog is to formulate the reasoning process as a function and represent each entity as a one-hot vector."⁸ This extends naturally to dense embeddings where entities become continuous vectors rather than discrete symbols.

Transformers Through the Tensor Logic Lens

The transformer architecture becomes remarkably interpretable through this lens.

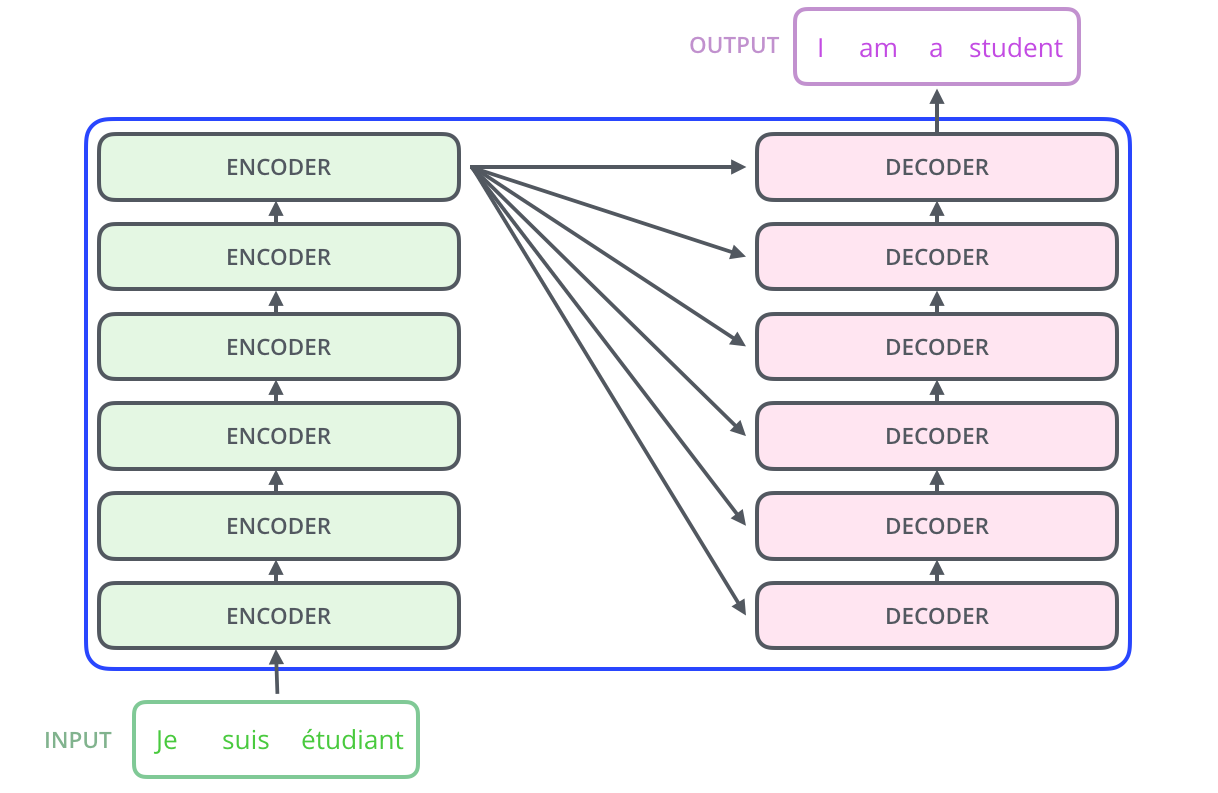Figure 3: The transformer architecture as a composition of tensor operations. "The encoding component is a stack of encoders (the paper stacks six of them on top of each other). The decoding component is a stack of decoders of the same number."⁹ Source: Jay Alammar, The Illustrated Transformer (jalammar.github.io)

Every operation in this stack is a tensor operation. "Each word is embedded into a vector of size 512. The embedding only happens in the bottom-most encoder."¹⁰ The self-attention layer creates Query, Key, and Value vectors, then computes attention weights through scaled dot products. "The first step in calculating self-attention is to create three vectors from each of the encoder's input vectors: a Query vector, a Key vector, and a Value vector."¹¹

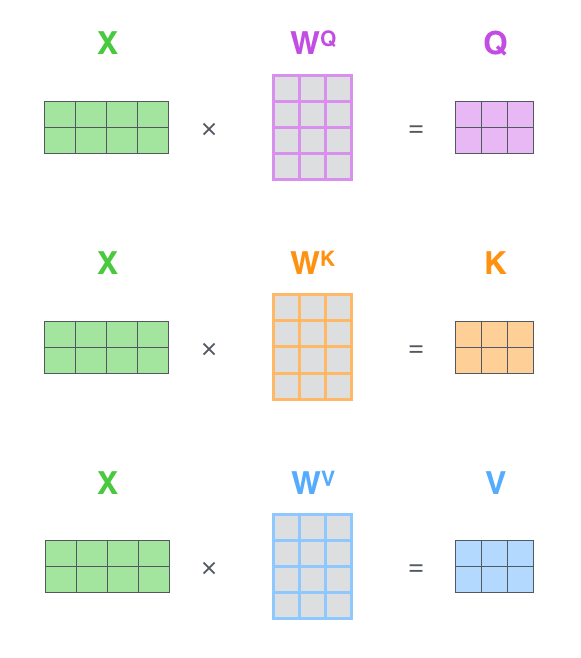Figure 4: Self-attention computed as matrix multiplication between queries and keys. "The score is calculated by taking the dot product of the query vector with the key vector of the respective word we're scoring."¹² Source: Jay Alammar, The Illustrated Transformer (jalammar.github.io)

In einsum notation, the attention calculation becomes elegant:

# Attention scores via einsum
scores = torch.einsum('bqd,bkd->bqk', Q, K)  # batch, query, key dimensions

The same notation expresses the multi-dimensional array operations in a single line that specifies which indices are contracted (summed over) and which are preserved. "The Transformer uses eight attention heads, so we end up with eight sets for each encoder/decoder."¹³ Each head performs the same tensor operation in parallel across different learned projections.

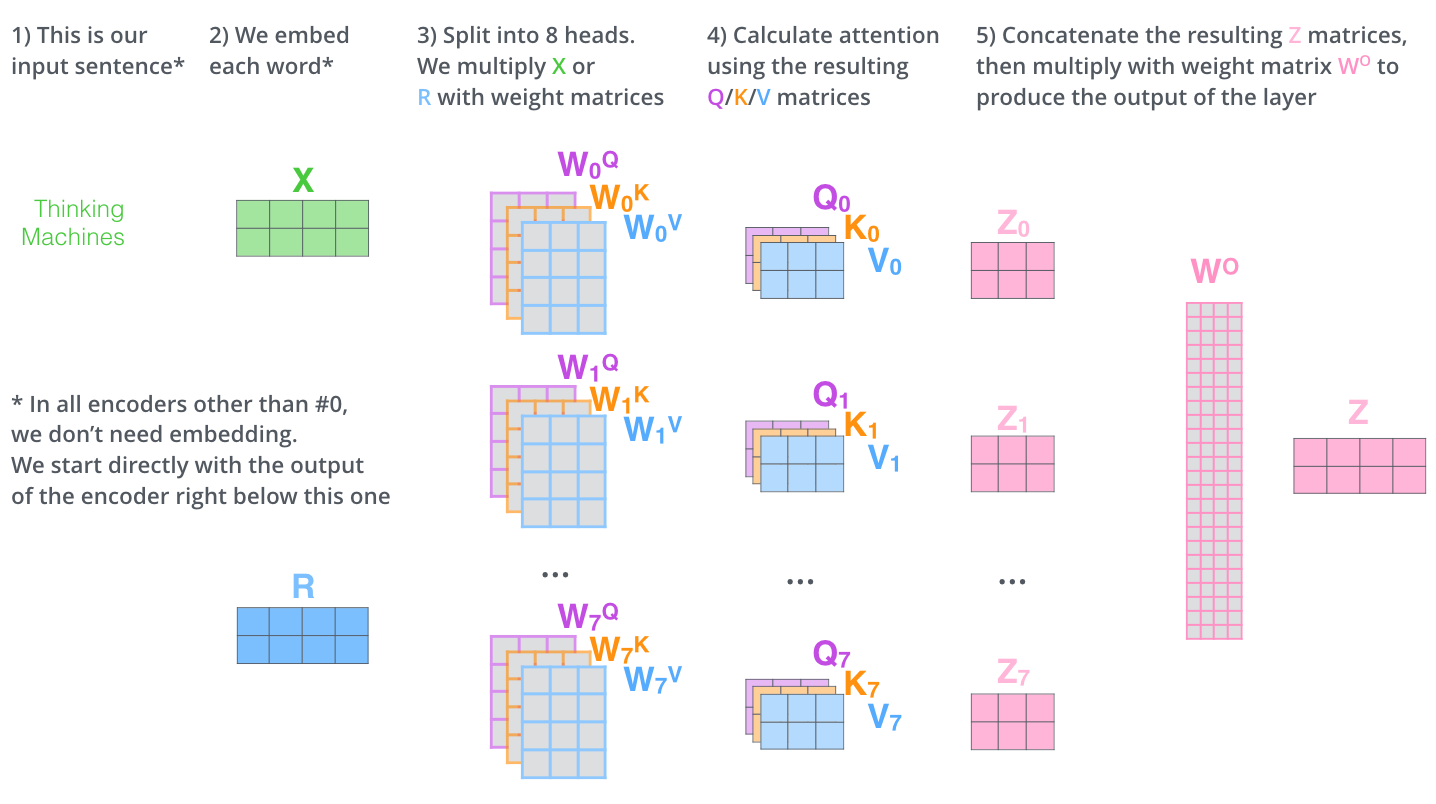Figure 5: Multi-head attention breaks the single attention operation into eight parallel computations, each a tensor contraction. Source: Jay Alammar, The Illustrated Transformer (jalammar.github.io)

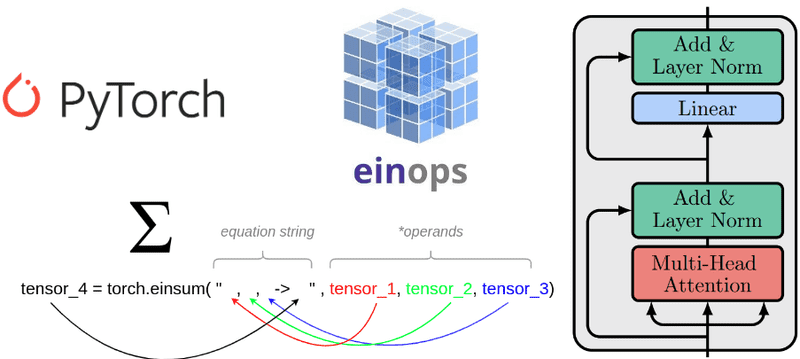Figure 6: Einstein summation notation in PyTorch directly implements the tensor contractions underlying transformer attention. Source: AI Summer, Understanding einsum for Deep Learning (theaisummer.com)

Tensor Networks: The Missing Link

The connection between neural networks and tensor operations has been developed extensively in the tensor network literature. "Tensor networks are a general means to efficiently represent higher-order tensors in terms of smaller tensor cores, in much the same way as UGMs [undirected graphical models] efficiently represent multivariate probability distributions in terms of smaller clique potentials."¹⁴

This isn't coincidence. "It was shown that the data defining a UGM is equivalent to that defining a TN, but with dual graphical notations that interchange the roles of nodes and edges."¹⁵ Probabilistic graphical models and tensor networks are mathematically equivalent formalisms with different notation.

Figure 7: Tensor train decomposition factorizes high-dimensional tensors into chains of lower-order tensors, enabling efficient computation. The same technique is used in quantum physics simulations and modern neural network compression. Source: PGM and Tensor Networks (arXiv:2106.15666), Figure 2

Born machines extend this further. "Born machines employ complex latent states that permit them to utilize novel forms of interference phenomena in structuring their learned distributions."¹⁶ "The probability distribution expressed by a fully-decohered Born machine with tensor cores A(v) is identical to that of a discrete undirected graphical model with clique potentials of the same shape."¹⁷

Figure 8: Born machines represent probability distributions through tensor network contractions, demonstrating the equivalence between probabilistic graphical models and tensor methods. Source: PGM and Tensor Networks (arXiv:2106.15666), Figure 3

The key insight: graphical models for probabilistic reasoning, tensor networks from quantum physics, and deep learning architectures are all computing with tensors. The differences lie in notation, not substance.

Higher-Order Transformers: Tensor Structure for Efficiency

Recent work on Higher Order Transformers exploits this insight directly. "We propose the Higher-Order Transformer (HOT), a novel factorized attention framework that represents multiway attention as sums of Kronecker products or sums of mode-wise attention matrices."¹⁸

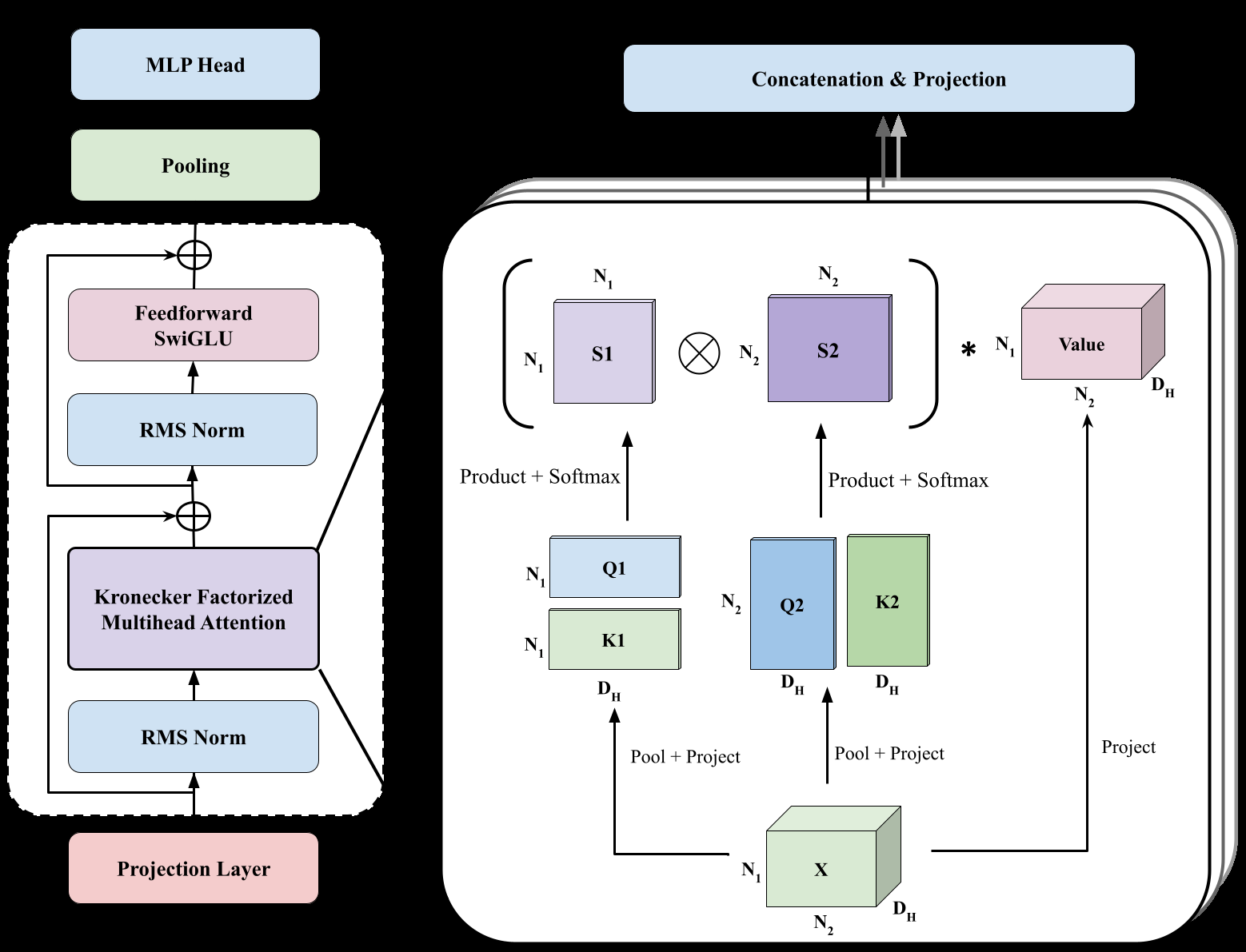Figure 9: The Higher Order Transformer architecture explicitly uses Kronecker factorization to handle multi-dimensional tensor data efficiently. Source: Higher Order Transformers (arXiv:2412.02919), Figure 1

The efficiency gains come from exploiting tensor structure that was always present but not formally acknowledged. "For an input of size 224^3, Kronecker attention requires only 371.6 GFLOPS, versus 775.3 GFLOPS for Full attention and 1210 GFLOPS for Divided attention."¹⁹ "HOT (product) requires only a third of the floating-point operations compared to non-factorized Transformer."²⁰

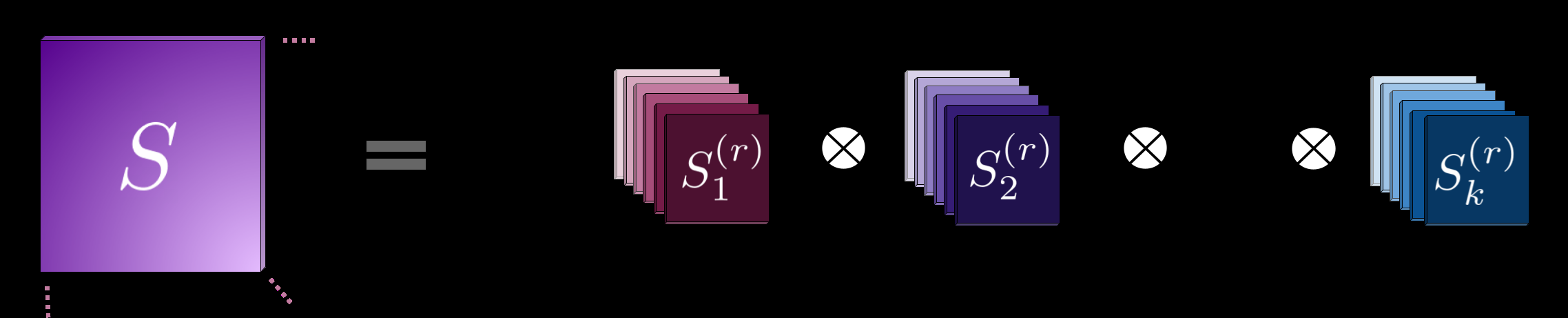Figure 10: Kronecker factorized attention decomposes high-dimensional attention into efficient per-axis computations, reducing complexity from quadratic in total size to quadratic in each axis dimension. Source: Higher Order Transformers (arXiv:2412.02919), Figure 2

The Shape of Reasoning

Here's where things get philosophical. If neural networks are performing tensor operations, and tensor operations are equivalent to logical inference, what does that tell us about reasoning itself?

One clue comes from topological analysis of neural networks. "As depth increases, a topologically complicated dataset is transformed into a simple one, resulting in Betti numbers attaining their lowest possible value."²¹ Networks learn to simplify the topology of their input space. They're finding structure.

Figure 11: Persistence diagrams showing how neural network layers progressively simplify the topological structure of embedding spaces. Source: Algebraic Topology of Embeddings (arXiv:2311.04592), Figure 1

This aligns with what logic does. Formal reasoning takes a complex mess of facts and relationships and finds the simpler structure that explains them. The syllogism "All humans are mortal; Socrates is human; therefore Socrates is mortal" reduces a complex question about Socrates's mortality to a simple traversal of logical structure.

Neural networks and logical systems might be doing the same thing in different languages. This is Domingos's deeper claim: not just that the notation is equivalent, but that the underlying computational operation is the same. Simplify, then traverse.

Knowledge Graphs and Embedding Space Reasoning

The neuro-symbolic community has already demonstrated that symbolic reasoning can happen in continuous embedding spaces. "The basic idea of TransE is to view the relation r as the transition from the head entity to the tail entity. Mathematically, it means that ideally, the tail entity t should be the summation of the head entity and the relation."²²

Figure 12: Knowledge graph embeddings project discrete symbolic entities into continuous vector spaces where neural operations perform relational reasoning. Source: Neural-Symbolic KG Reasoning Survey (arXiv:2412.10390), Figure 3

More sophisticated approaches like Query2Box "model queries as boxes (i.e., hyper-rectangles), where a set of points inside the box corresponds to a set of answer entities of the query."²³ NeuralLP generalizes TensorLog with learned confidence scores, where "the reasoning process is a sequence of matrix multiplication operations."²⁴

These systems perform sound logical inference through tensor operations. The logical structure is preserved. The computation is neural.

The Limitations Question

The honest answer is we don't fully know what the limitations are.

Single-vector embeddings have proven theoretical limitations. Research has shown "there exists some tasks that embedding models will never be able to solve" for instruction-following and reasoning.²⁵ But tensor logic isn't limited to single vectors. The full tensor structure preserves information that collapses in vector projections.

The optimization question remains open. Training systems that must satisfy both gradient-based learning objectives and logical consistency constraints is hard. Current neuro-symbolic systems use various compromises. DeepStochLog "enhances traditional logic programming with neural networks for complex reasoning tasks."²⁶ Logical Credal Networks combine "logical reasoning with probabilistic models to handle imprecise information."²⁷ Each makes different tradeoffs.

Scalability is untested at the largest scales. Research on neuro-symbolic AI "is increasing exponentially starting in 2020, with notable increases from 2020 (53 publications), and peaking in 2023 (236 publications)."²⁸ But most implementations remain research prototypes. Production deployment at GPT-4 scale hasn't happened.

What Changes

If Domingos is right, several things follow.

First, the tooling problem simplifies. Instead of PyTorch for learning and Prolog for reasoning and Stan for inference, you get one language. The tensor equation serves as the universal intermediate representation. Optimizations in one domain transfer to all domains.

Second, the theoretical foundations unify. Currently, neural network theory and symbolic AI theory are separate fields with separate conferences and separate journals. Tensor logic provides a shared mathematical substrate. Results about tensor operations apply to both learning and reasoning.

Third, new architectures become possible. When you recognize that a transformer and a theorem prover are computing the same kinds of things, you can mix components freely. Attention over logical formulas. Inference over embedding spaces. Kernel methods applied to logical structures.

The practical question is whether this recognition enables anything new. Can we build systems that genuinely reason in embedding space with logical soundness? Can we learn logical rules from data as efficiently as neural networks learn features? Can we combine the reliability of formal methods with the flexibility of deep learning?

The research suggests we can, but the production implementations don't exist yet. The tensor logic framework gives us a language to try.

I'm curious whether the bottleneck is mathematical, computational, or sociological. The math seems to work. The compute exists. But AI research remains fragmented. Perhaps tensor logic is the language that finally lets the tribes talk to each other.

---

References

Footnotes

1. Domingos, P. (2025). "Tensor Logic: The Language of AI." arXiv:2510.12269. Lines 14-18. ↩

2. Neuro-Symbolic AI in 2024: A Systematic Review. arXiv:2501.05435. 167 papers analyzed on neuro-symbolic approaches. ↩

3. Domingos, P. (2025). "Tensor Logic: The Language of AI." arXiv:2510.12269. Lines 25-30. ↩

4. Neuro-Symbolic AI in 2024: A Systematic Review. arXiv:2501.05435. Lines 22-24. ↩

5. Neuro-Symbolic AI in 2024: A Systematic Review. arXiv:2501.05435. Lines 235-340. ↩

6. Manhaeve, R. et al. (2018). "DeepProbLog: Neural Probabilistic Logic Programming." arXiv:1805.10872. Lines 14-23. ↩

7. Neural-Symbolic Reasoning over Knowledge Graphs Survey. arXiv:2412.10390. Lines 79-85. ↩

8. Neural-Symbolic Reasoning over Knowledge Graphs Survey. arXiv:2412.10390. Lines 264-268. ↩

9. Alammar, J. "The Illustrated Transformer." jalammar.github.io. Line 213. ↩

10. Alammar, J. "The Illustrated Transformer." jalammar.github.io. Lines 246-249. ↩

11. Alammar, J. "The Illustrated Transformer." jalammar.github.io. Lines 299-300. ↩

12. Alammar, J. "The Illustrated Transformer." jalammar.github.io. Lines 320-321. ↩

13. Alammar, J. "The Illustrated Transformer." jalammar.github.io. Lines 392-393. ↩

14. PGM and Tensor Networks Hybrid. arXiv:2106.15666. Lines 152-154. ↩

15. PGM and Tensor Networks Hybrid. arXiv:2106.15666. Lines 281-283. ↩

16. PGM and Tensor Networks Hybrid. arXiv:2106.15666. Lines 55-57. ↩

17. PGM and Tensor Networks Hybrid. arXiv:2106.15666. Lines 409-412. ↩

18. Higher Order Transformers. arXiv:2412.02919. Lines 21-23. ↩

19. Higher Order Transformers. arXiv:2412.02919. Lines 691-697. ↩

20. Higher Order Transformers. arXiv:2412.02919. Lines 546-548. ↩

21. Algebraic Topology of Embeddings. arXiv:2311.04592. Lines 18-20. ↩

22. Neural-Symbolic Reasoning over Knowledge Graphs Survey. arXiv:2412.10390. Lines 355-359. ↩

23. Neural-Symbolic Reasoning over Knowledge Graphs Survey. arXiv:2412.10390. Lines 530-533. ↩

24. Neural-Symbolic Reasoning over Knowledge Graphs Survey. arXiv:2412.10390. Lines 344-351. ↩

25. Weller, O., Boratko, M., Naim, I., & Lee, J. (2024). "Limitations of Embedding-Based Retrieval for Multi-hop Question Answering." arXiv:2508.21038. ↩

26. Neuro-Symbolic AI in 2024: A Systematic Review. arXiv:2501.05435. Lines 310-311. ↩

27. Neuro-Symbolic AI in 2024: A Systematic Review. arXiv:2501.05435. Lines 309-310. ↩

28. Neuro-Symbolic AI in 2024: A Systematic Review. arXiv:2501.05435. Lines 165-167. ↩