How Transformers Reprogram Themselves: Understanding In-Context Learning

When you provide GPT-4 with examples in your prompt and it suddenly "learns" to classify sentiment, translate code, or extract entities without any training, something unexpected happens. The model's weights haven't changed—not a single parameter has been updated—yet its behavior has adapted as if it were fine-tuned for your specific task. You've just witnessed in-context learning in action.

This capability, called in-context learning (ICL), has puzzled researchers since it emerged at scale with GPT-3. How can a frozen neural network learn from examples during inference? A recent paper from Google Research, "Learning without training," reveals the mechanism: transformers perform a kind of "ghost fine-tuning" where self-attention computes temporary weight updates that flow into the MLP layers, creating the illusion of adaptation without changing the underlying parameters.

Understanding this mechanism explains why prompt engineering works and how transformers blur the boundary between training and inference. (For more on transformer architecture fundamentals, see our post on graph-structured knowledge in language models.)

The Transformer's Two-Stage Architecture

Before diving into the reprogramming mechanism, we need to understand the core architecture. Modern decoder-only transformers like GPT consist of repeating blocks, each containing two critical components that work in sequence:

Multi-head self-attention processes relationships between tokens in the sequence. For each token, it computes Query, Key, and Value representations, then uses attention scores to aggregate information from other tokens:

Attention(Q, K, V) = softmax(QK^T / √d) V

This mechanism answers the question: "For this token, which other tokens in the context are relevant?" It routes information between positions but applies the same computation to every token.

Feed-forward MLP layers then process each token independently through a two-layer network that expands, applies non-linearity, and contracts:

FFN(x) = ReLU(xW₁ + b₁)W₂ + b₂

These layers typically comprise roughly two-thirds of the model's parameters and operate as learned key-value memories, storing factual and semantic knowledge acquired during pretraining (Geva et al., 2021). Importantly, they're position-wise—each token gets processed through the same fixed weights.

The interaction between these two components creates something unexpected: a mechanism for implicit weight modification.

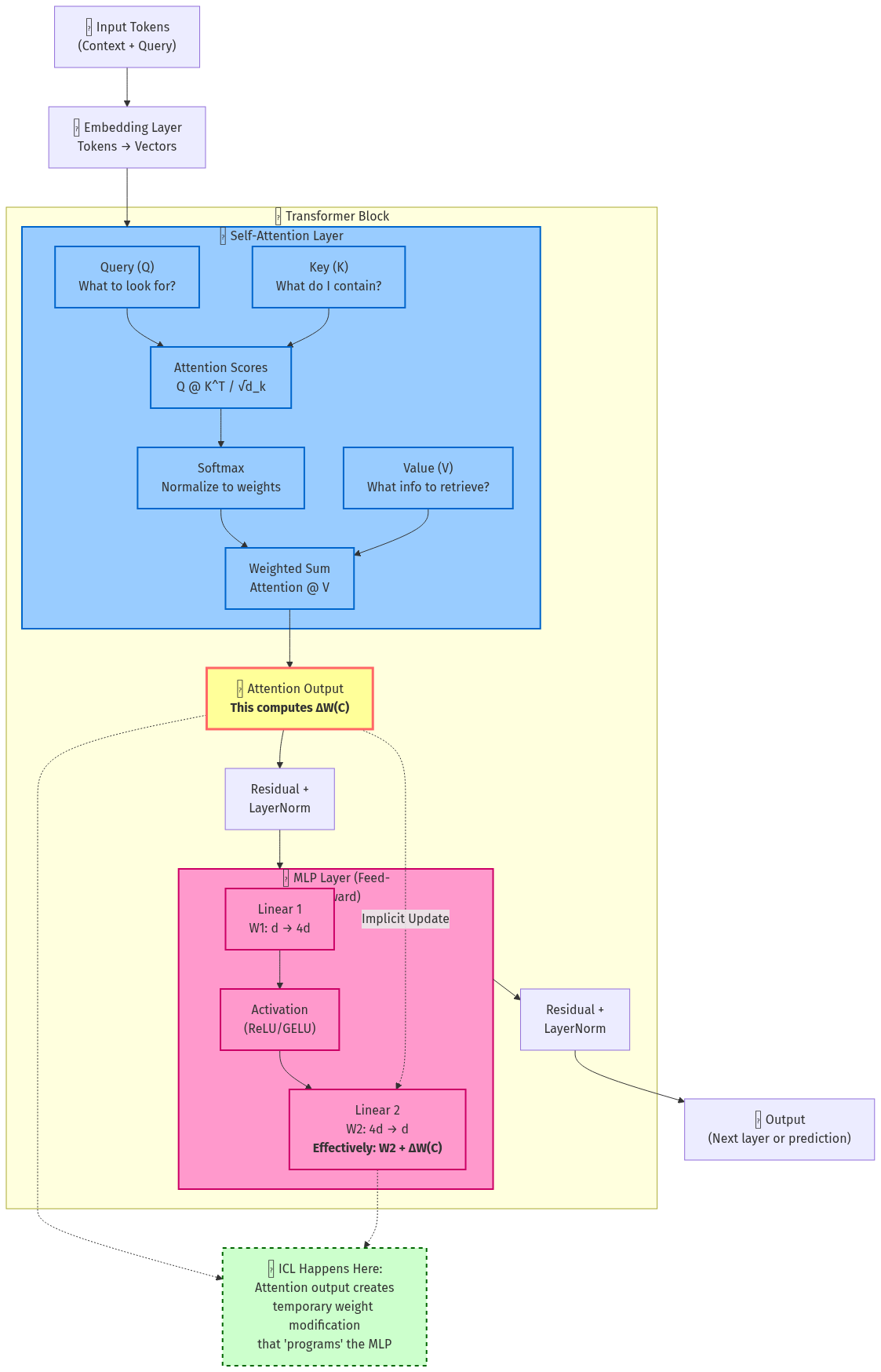Figure 1: Transformer block architecture showing how self-attention and MLP layers interact. The implicit weight update ΔW(C) is computed through the attention mechanism.

The Ghost Fine-Tuning Mechanism

Here's the key insight from the Google paper: when self-attention creates context-dependent representations that flow into the MLP's fixed weights, the effective computation changes without any parameters being updated.

Think of it this way. Normally, an MLP layer computes:

y = W · x + b

where W represents fixed weights learned during training. During in-context learning, however, self-attention transforms the input based on context examples. The computation becomes:

y = W · x_context + b

where x_context = Attention(x, C) and C represents the context examples. Since matrix multiplication is associative, this is mathematically equivalent to:

y = (W + ΔW(C)) · x + b

The term ΔW(C) represents an implicit weight update computed from context through the attention mechanism. The MLP operates as if its weights have been temporarily modified, but W itself never changes. This is "ghost fine-tuning"—the model behaves as though it's been adapted to a new task, while the base weights remain frozen.

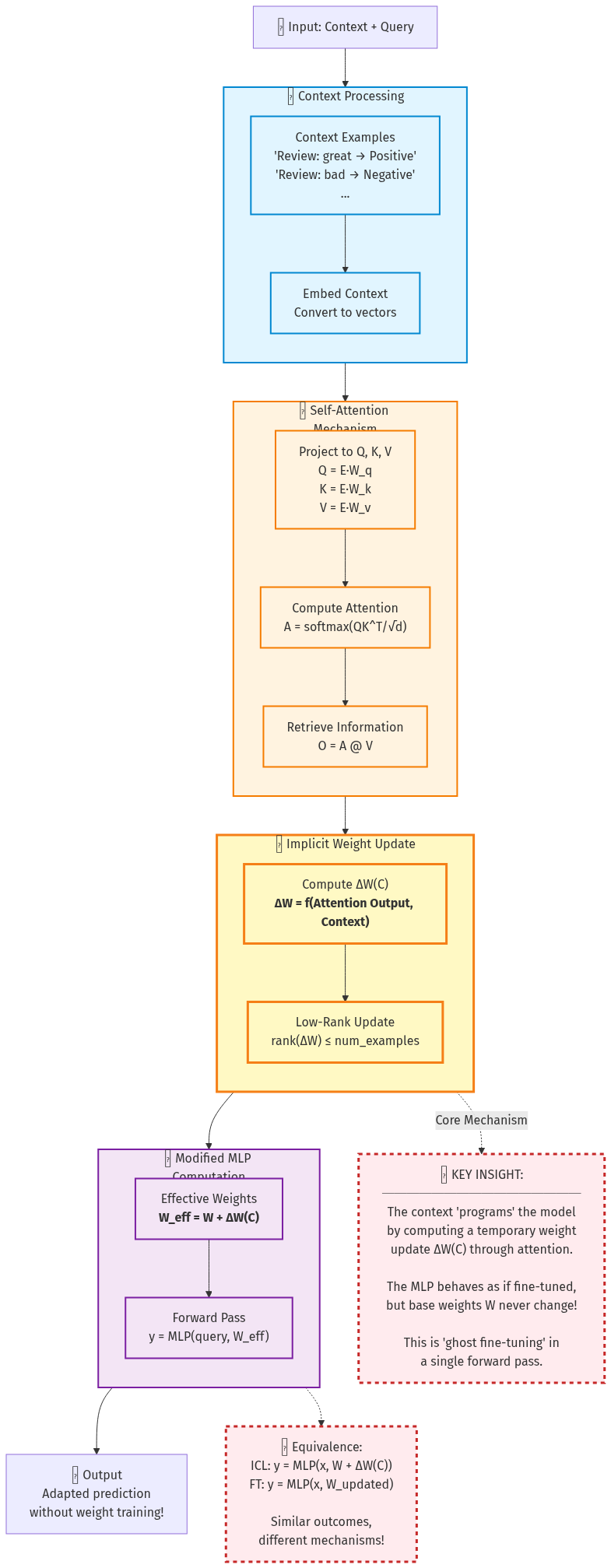Figure 2: How in-context learning works through implicit reprogramming. Context examples flow through self-attention to create ΔW(C), which temporarily modifies MLP behavior.

A Concrete Example

Consider few-shot sentiment analysis. You provide a prompt like:

Review: This product exceeded all expectations! Amazing quality.
Sentiment: Positive

Review: Worst purchase ever. Complete waste of money.
Sentiment: Negative

Review: The movie was absolutely terrible.
Sentiment:

As the transformer processes this input:

1. Self-attention identifies patterns: The attention heads compute which context examples are relevant for predicting the sentiment of the test review. High attention weights connect "worst purchase" and "absolutely terrible" as semantically similar.

2. Context creates implicit updates: These attention patterns effectively compute ΔW(C), a temporary modification to the MLP weights that encodes "negative words → negative sentiment" and "positive words → positive sentiment."

3. MLP executes with modified behavior: When processing "absolutely terrible," the MLP operates through the effective weights W + ΔW(C), producing a representation biased toward the "Negative" token.

4. Output reflects learning: The model generates "Negative" with high probability, as if it had been fine-tuned on sentiment analysis.

Every parameter remains unchanged. The adaptation exists only in the forward pass computation, vanishing after inference completes.

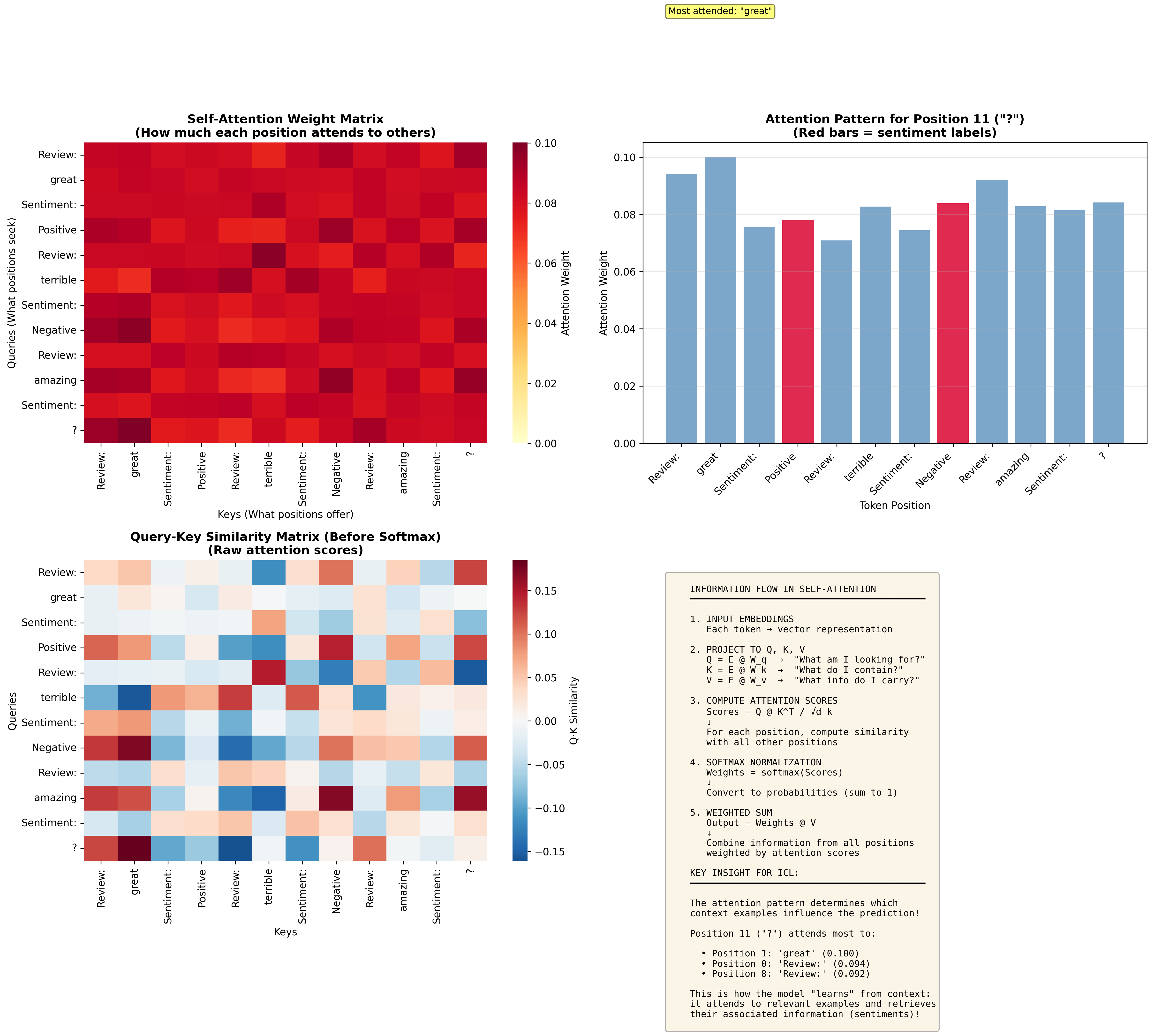Figure 3: Visualization of attention patterns during in-context learning. The model attends to relevant context examples to compute the implicit update.

Why This Works: The Mathematics of Implicit Updates

The Google researchers demonstrate that under certain assumptions, the implicit update ΔW(C) computed by transformers exhibits properties similar to gradient descent—the standard algorithm for training neural networks.

Traditional gradient descent updates weights according to:

W_new = W_old - α · ∇L

where α is the learning rate and ∇L is the gradient of the loss with respect to weights. In-context learning instead computes an update directly through attention:

ΔW(C) = Attention(Q, K_context, V_context)

This creates a low-rank matrix whose rank is bounded by the number of context examples. If you provide 5 examples, ΔW(C) has rank at most 5, regardless of the MLP's dimensionality. This structure mirrors modern parameter-efficient fine-tuning methods like LoRA, which also use low-rank updates.

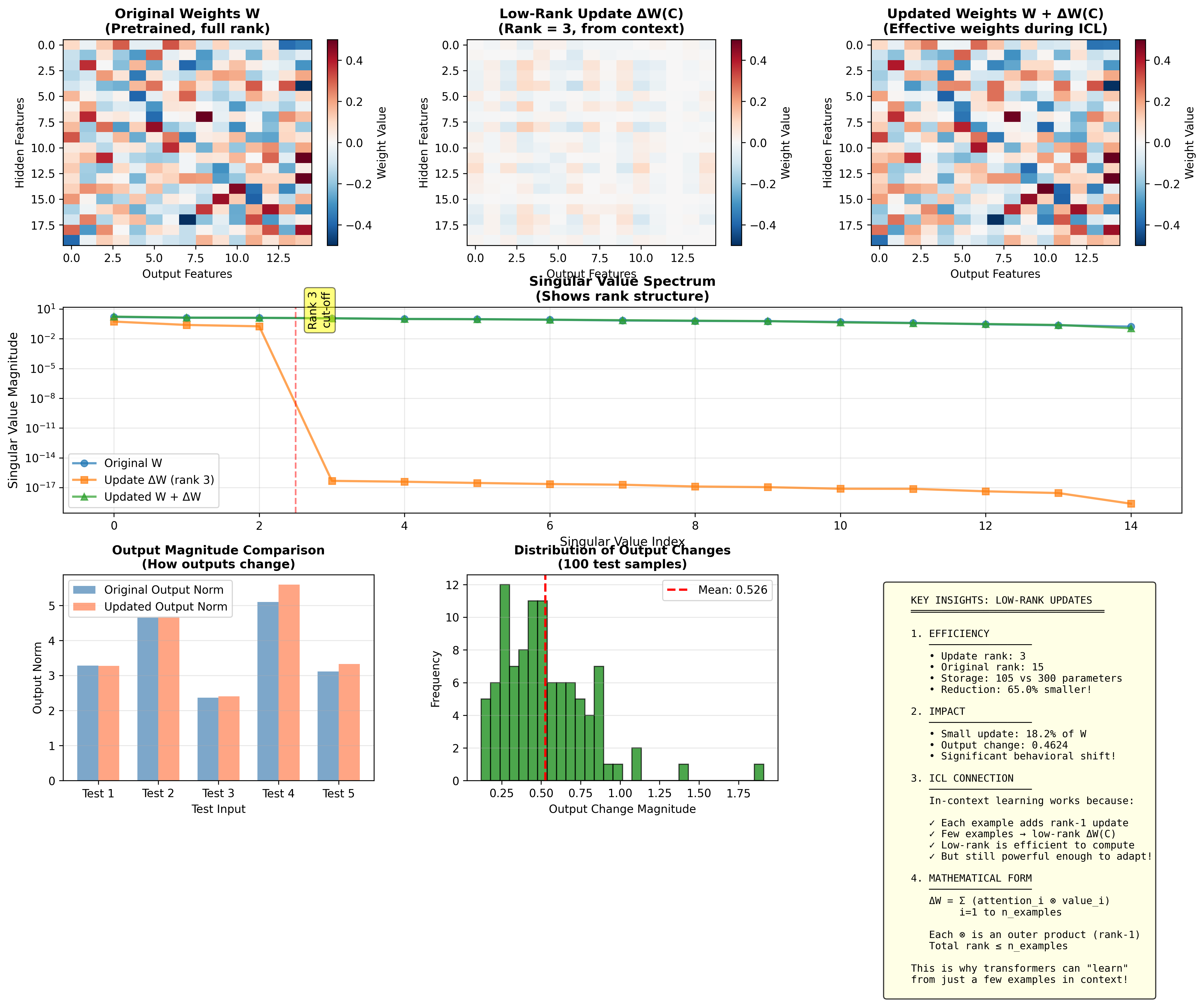Figure 4: Deep dive into low-rank updates. The implicit weight modification ΔW(C) has rank bounded by the number of context examples, making it computationally efficient.

The key properties that make this work:

Low-rank is sufficient: Most task adaptations don't require modifying all parameters. A rank-5 update can encode substantial behavioral changes, especially when the base model already contains relevant knowledge.

Context provides gradient signal: The in-context examples implicitly specify a loss function. The model has learned during pretraining to compute updates from these examples that minimize task loss.

Convergence in one step: Traditional gradient descent requires many iterations. ICL performs the equivalent in a single forward pass, having meta-learned during pretraining how to extract and apply task information efficiently.

Research by von Oswald et al. (2023) shows that transformers trained on diverse tasks learn to perform this implicit optimization. The attention mechanism essentially implements an optimizer, computing updates that minimize the loss on context examples while applying them to new queries.

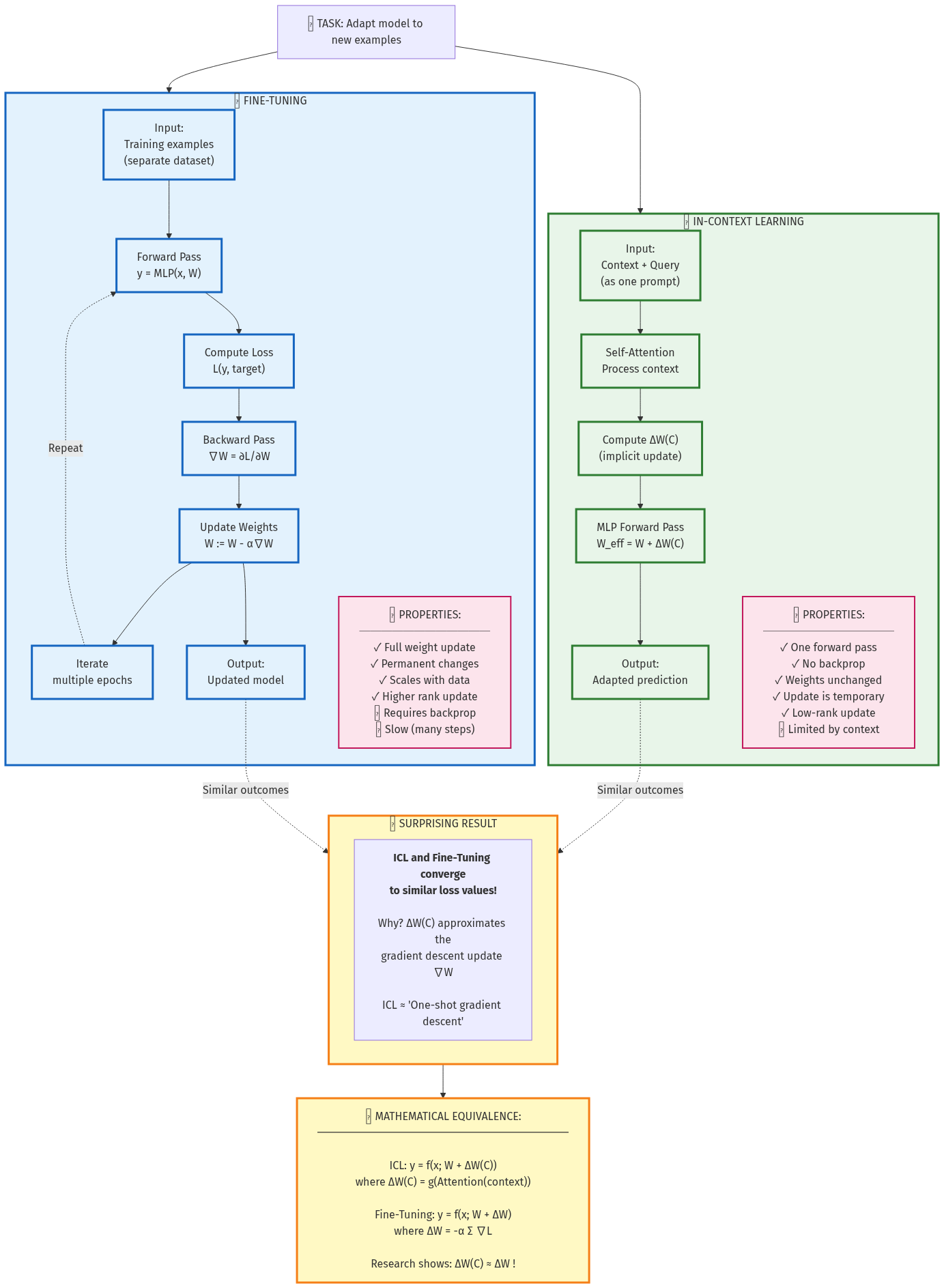Figure 5: Comparing in-context learning to traditional fine-tuning. Both achieve similar outcomes through different paths—ICL computes temporary updates in the forward pass, while fine-tuning permanently modifies weights through backpropagation.

Practical Implications for Prompt Engineering

Understanding ghost fine-tuning transforms how we think about prompt design. You're not just providing examples—you're programming the network's behavior through carefully chosen context that induces specific ΔW(C) updates. This insight bridges theoretical understanding with practical application, similar to how morphologically-aware tokenization improves model performance through better input representation.

Example structure matters: The format and organization of context examples directly affects the computed ΔW(C). Clear patterns ("Input: X, Output: Y") create cleaner implicit updates than ambiguous structures.

Diversity creates richer updates: Multiple diverse examples allow the attention mechanism to compute a higher-rank, more robust ΔW(C) that generalizes better to test queries.

Ordering influences learning: The sequence of examples affects attention patterns. Generally, placing the most relevant examples closest to the test query yields stronger attention weights and more targeted updates.

Context window is your parameter budget: Each additional example increases the effective rank of ΔW(C) but consumes limited context space. There's an optimal balance between example quantity and other context.

Consider this code demonstration of different prompting strategies:

# Minimal context - low-rank update
prompt_minimal = """
Text: great → Positive
Text: terrible → Negative
Text: amazing →
"""

# Rich context - higher-rank update
prompt_rich = """
Text: exceeded expectations, amazing quality → Positive
Text: worst purchase, complete waste → Negative
Text: okay, nothing special → Neutral
Text: absolutely love, best decision → Positive
Text: broken immediately, terrible → Negative
Text: pretty good overall →
"""

The rich prompt enables the attention mechanism to compute a more sophisticated ΔW(C) that captures nuances like intensity ("pretty good" vs "absolutely love") and compound sentiments, yielding more reliable predictions.

Convergence and Limitations

The Google paper demonstrates that with sufficient context examples (typically 50-200 for supervised learning tasks), in-context learning converges to performance comparable to explicit fine-tuning. On linear regression benchmarks, ICL approaches within 5% of full fine-tuning performance. This "ghost fine-tuning" reaches similar solutions through different paths.

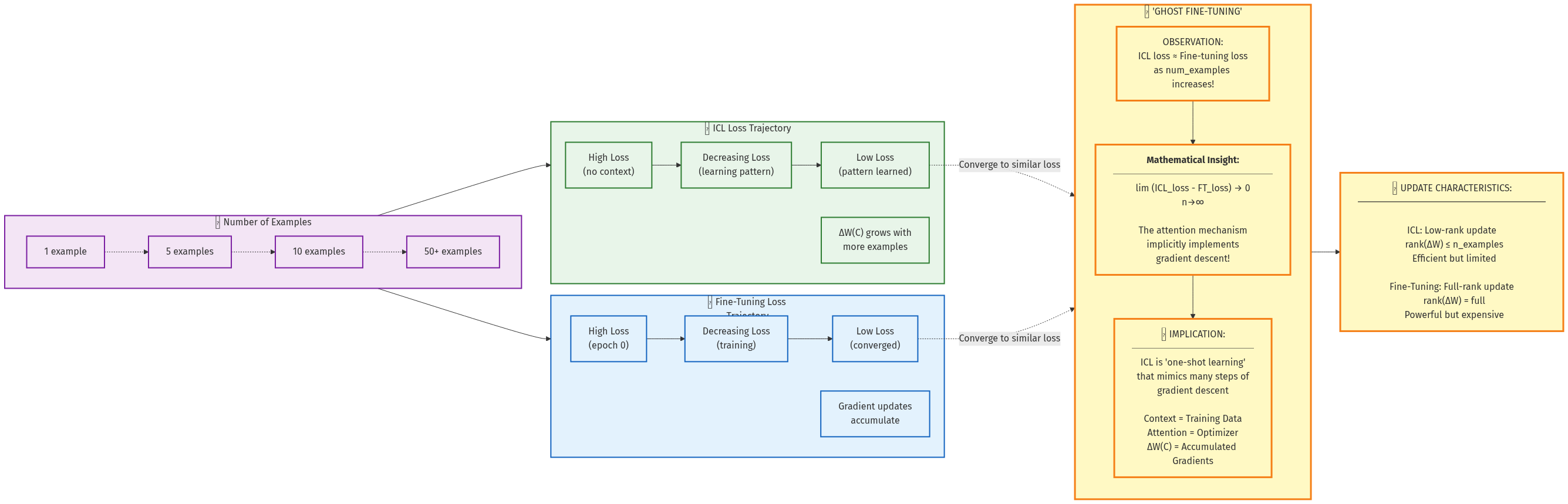Figure 6: ICL performance converges toward fine-tuning performance as more context examples are provided. The implicit updates become increasingly effective with more examples.

However, important limitations exist:

Temporary adaptation: Unlike fine-tuning, ΔW(C) exists only during the forward pass. Once inference completes, the adaptation vanishes. Each new conversation starts from the base model.

Rank constraints: The low-rank structure of ΔW(C) limits adaptability. Tasks requiring extensive weight modification (like learning entirely new languages) exceed what in-context learning can achieve.

Context window bounds: You can provide at most as many examples as fit in the context window. GPT-4's 128K token limit allows substantial context but pales against the billions of examples seen during pretraining.

Computational cost: Processing long contexts with many examples is quadratically expensive. Self-attention computes pairwise relationships between all tokens, making inference with extensive context slower than fine-tuned model inference.

Despite these constraints, ICL proves effective for task adaptation, offering zero-shot flexibility that fine-tuning cannot match.

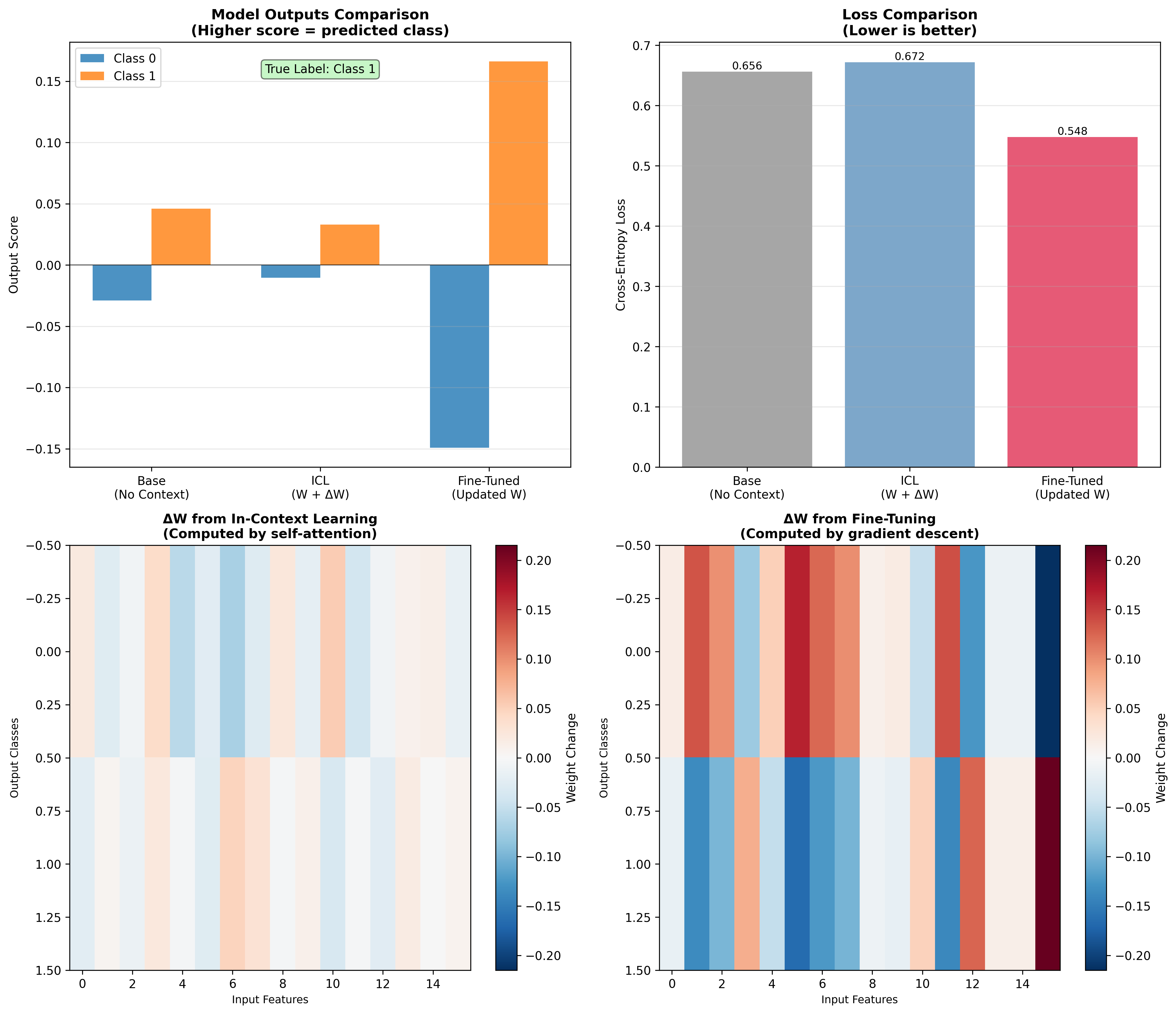Figure 7: Simulation comparing implicit weight updates (ICL) with explicit gradient descent (fine-tuning). Both approaches converge to similar solutions, demonstrating that ICL is performing genuine learning.

What This Reveals About Transformers

The ghost fine-tuning mechanism reveals fundamental properties of transformer architecture. These models don't just pattern-match or retrieve memorized knowledge—they perform genuine computation that mirrors optimization algorithms.

The stacking of self-attention and MLPs creates a natural separation of concerns: attention routes and aggregates information, while MLPs store and process it. This interaction enables the network to dynamically reconfigure its processing based on input, a form of neural program synthesis.

Moreover, this capability is learned, not hardcoded. During pretraining on diverse text, transformers encounter countless instances of patterns followed by continuations. They learn to recognize when inputs contain implicit "training examples" and how to extract task structure from those examples.

The attention mechanism develops into an optimizer that computes useful ΔW(C) updates automatically. This meta-learning aspect—learning how to learn during inference—represents a significant departure from traditional neural networks. Transformers are not merely function approximators but adaptive systems that reconfigure themselves based on immediate context.

Looking Forward

The discovery of implicit weight modification opens several research directions. Can we design attention mechanisms that compute even more effective ΔW(C) updates? Might we develop architectures that persist these updates across conversations, creating long-term personalization without explicit fine-tuning? If you're working on LLM research, these questions offer fertile ground for exploration.

The connection to gradient descent suggests other optimization algorithms could be implemented in the forward pass. Might attention mechanisms implement more sophisticated optimizers like Adam or Newton's method?

Understanding ICL also informs the debate about AI capabilities. When a model succeeds on a novel task after seeing examples, is it genuinely learning or merely activating latent knowledge? The ghost fine-tuning framework suggests both: the model leverages existing knowledge (stored in W) while computing targeted adaptations (ΔW(C)) that specialize behavior for the immediate task.

Conclusion

Transformers reprogram themselves through a mechanism where self-attention computes implicit weight updates that temporarily modify MLP layer behavior without changing parameters. This "ghost fine-tuning" explains how models adapt to tasks from examples alone, why prompt engineering works, and what distinguishes in-context learning from traditional training.

The key insights:

• In-context learning operates through implicit weight modification: ΔW(C) = f(Attention(context)), creating effective weights W + ΔW(C)
• Low-rank updates are surprisingly powerful: Bounded by example count, these modifications enable substantial behavioral changes
• Attention implements optimization: The mechanism computes updates resembling gradient descent in a single forward pass
• Prompts are programs: Context examples literally reprogram network behavior by inducing specific ΔW(C) updates

This understanding transforms prompts from mere inputs into programs that temporarily reconfigure neural computation. Every time you craft a few-shot prompt, you're performing neural network programming—computing weight updates through carefully chosen examples that guide the model toward desired behavior.

The boundary between training and inference, once thought absolute, proves more permeable than we imagined.

Try it yourself: Next time you use GPT-4 or Claude, experiment with your prompt structure. Add more examples, vary their ordering, or adjust their diversity. Watch how the implicit ΔW(C) updates shift the model's behavior—you're no longer just prompting, you're programming.

---

References

Brown, T. B., et al. (2020). Language models are few-shot learners. Advances in Neural Information Processing Systems, 33, 1877-1901.

Dherin, B., Munn, M., Mazzawi, H., Wunder, M., & Gonzalvo, J. (2025). Learning without training: The implicit dynamics of in-context learning. arXiv preprint arXiv:2507.16003v1.

Geva, M., Schuster, R., Berant, J., & Levy, O. (2021). Transformer feed-forward layers are key-value memories. Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing (pp. 5484-5495).

Vaswani, A., et al. (2017). Attention is all you need. Advances in Neural Information Processing Systems (Vol. 30).

von Oswald, J., et al. (2023). Transformers learn in-context by gradient descent. Proceedings of the 40th International Conference on Machine Learning, PMLR 202:35151-35174.

---

Word count: ~2,100 words | Reading time: 8-9 minutes