When you add the vector for "king" minus the vector for "man" plus the vector for "woman," you get something close to "queen." This famous result from Word2Vec sparked a fascinating question: if word embeddings can capture semantic relationships through simple vector arithmetic, can they do the same for grammar? Specifically, is there a consistent "tense axis," a single direction in the embedding space that transforms verbs from present to past tense?
This investigation takes you on a journey from the theoretical foundations of distributed semantics to hands-on experiments with real Word2Vec embeddings. We'll explore whether the elegant geometric patterns discovered in early embedding models still hold true in modern contextual models like BERT, and what this tells us about how AI represents language.
From Words to Vectors: The Foundation of Distributed Semantics
The expectation that grammatical structure might emerge geometrically isn't arbitrary. It's rooted in a fundamental principle of linguistics. If you compiled a massive list of every sentence where the word "coffee" appears, and another list for "tea," you'd notice they share similar contexts. Both appear near words like "cup," "hot," "drink," and "morning." This observation is the distributional hypothesis: words that occur in similar contexts tend to have similar meanings.
Word embedding models operationalize this principle by constructing a co-occurrence matrix. Imagine a giant spreadsheet where each row represents a word from your vocabulary, and each column represents a "context word." The entry at row , column counts how many times word appears within, say, 5 words of word throughout an entire corpus. For instance, if you're looking at the row for "swim," you might see high counts in columns for "pool," "water," and "ocean." This matrix becomes the raw material from which dense, low-dimensional word vectors are learned.
Two landmark models pioneered this approach:
Word2Vec, developed at Google, uses a shallow neural network to learn embeddings as a byproduct of prediction tasks. Its Skip-Gram variant, for example, tries to predict surrounding context words from a target word. As the network trains through backpropagation, words that appear in similar contexts naturally end up with similar vectors. Not because the model was told to do this, but because similar vectors help it make better predictions. The embeddings themselves are simply the learned weights of the network's hidden layer.
GloVe (Global Vectors), created at Stanford, takes a different tack. Instead of predicting local contexts, GloVe optimizes word vectors so their dot product equals the logarithm of their co-occurrence probability. The insight here is elegant: ratios of co-occurrence probabilities encode meaning. Consider , this ratio will be large, revealing the relationship between "solid" and "ice." GloVe's training objective explicitly connects vector geometry to global statistical structure.
The Emergence of Linear Structure: Analogies as Geometric Translations
The most striking discovery from these models wasn't just that similar words ended up close together. It was that meaningful directions emerged in the space. The operation vector('king') - vector('man') + vector('woman') yields a vector nearest to vector('queen'). Geometrically, this suggests that vector('king') - vector('man') represents a "royalty vector," while vector('woman') - vector('man') captures a "gender vector."
This linear structure isn't programmed in. It's emergent. Word2Vec's training objective simply encourages co-occurring words to have similar vectors. Yet language itself contains deep statistical regularities. The word "queen" appears in contexts similar to "king" (words like "royal," "throne," "reign") and contexts similar to "woman" (pronouns like "she," "her"). To minimize prediction error across the entire corpus, the most efficient solution is to place "queen" at a position that can be represented as a linear combination: vector('king') + vector('gender_offset').
This principle extends to grammatical relationships. Researchers found that models could capture pluralization (apple → apples) and verb tense (walk → walked, sing → sang) through similar vector operations. This is where the "tense axis" hypothesis originates: if a consistent vector offset exists that transforms any verb from one tense to another, then grammar has a geometric reality in these embedding spaces.
However, the quality of any discovered "axis" depends entirely on how consistently that linguistic feature appears in training data. If past and present tense verbs frequently appear in interchangeable contexts, the resulting "tense vector" will be noisy and unreliable.
Probing the Latent Space: Scientific Methods for Testing the Hypothesis
While vector analogies provide compelling anecdotal evidence, the field of NLP demanded more rigorous methods. This led to probing tasks, supervised classification experiments designed to systematically investigate what linguistic information embeddings actually encode.
Probing works like this: you take frozen (non-trainable) embeddings from a pre-trained model and use them as input features to train a simple classifier, like logistic regression. This classifier tries to predict a specific linguistic label, say, whether a verb is past or present tense. If a simple classifier achieves high accuracy, it means the information required for that prediction is linearly separable in the embedding space.
The key insight is that probing measures information already present in the embeddings, rather than teaching a complex model to solve the task from scratch. The success of the probe serves as a quantitative measure of encoding quality.
Studies using this methodology have yielded fascinating results. Conneau et al. (2018) introduced a suite of ten probing tasks, one of which was Tense classification. They found that sentence encoders pre-trained on machine translation could accurately classify tense, demonstrating that this information was captured as a byproduct of the original training objective. Follow-up work by Bacon & Regier (2018) specifically investigated main clause tense in RNNs, testing whether models learned true syntactic rules or surface-level heuristics.
More recently, a 2024 study on BERT and GPT-2 explored verb aspect, properties like whether an event is ongoing or completed. The researchers found that stativity (state vs. event) and telicity (having a natural endpoint) were consistently encoded, though durativity proved more elusive.
However, there's a critical distinction to understand: probing success demonstrates linear separability, not the simple vector offset hypothesis. Linear separability means a hyperplane can separate past tense verbs from present tense verbs. The "tense axis" hypothesis makes a stronger claim: that vector(verb_past) ≈ vector(verb_present) + vector(tense_offset), where tense_offset is constant across all verbs. It's geometrically possible for two clouds of points to be perfectly separable by a plane, yet the vectors connecting corresponding points within those clouds can point in many different directions.
This distinction motivates the hands-on investigation that follows, we need to visualize these offset vectors directly to see if they truly align.
Testing the Tense Axis: A Hands-On Exploration
To move from theory to empirical evidence, we can run actual experiments with Word2Vec embeddings. Using Python and the gensim library, we can load the pre-trained word2vec-google-news-300 model (trained on 3 million words and phrases with 300-dimensional vectors) and test tense analogies directly.
Replicating Tense Analogies
A simple experiment testing four tense transformations:
import gensim.downloader as api
# Load pre-trained Word2Vec model
wv = api.load('word2vec-google-news-300')
def solve_analogy(positive_terms, negative_terms):
"""Solves: A : B :: C : ?"""
return wv.most_similar(positive=positive_terms, negative=negative_terms, topn=1)
# Test cases
print(solve_analogy(['walk', 'swimming'], ['walking']))
# Output: ('swim', 0.8260)
print(solve_analogy(['walk', 'played'], ['walked']))
# Output: ('play', 0.7124)
print(solve_analogy(['swim', 'thought'], ['swam']))
# Output: ('think', 0.6145)
print(solve_analogy(['sang', 'eat'], ['sing']))
# Output: ('ate', 0.7839)
The results are striking. In each case, the model correctly identifies the corresponding verb form with high similarity scores (ranging from 0.61 to 0.83). This confirms that Word2Vec captures grammatical relationships through consistent vector operations, for both regular verbs like "walk/walked" and irregular verbs like "sing/sang."
Visualizing the Geometry with PCA
To test the "tense axis" hypothesis directly, we need a visualization method that preserves global linear relationships. Principal Component Analysis (PCA) is perfect for this. PCA is a linear dimensionality reduction technique that projects high-dimensional data onto new orthogonal axes (principal components) that capture maximum variance. Because it's a linear projection, parallel vectors in the original 300-dimensional space will remain parallel in the 2D projection.
The experiment: we select five verbs (walk, swim, think, drive, fly) and their conjugated forms (base, -ing, past). After extracting their 300-dimensional vectors and reducing them to 2D via PCA, we draw arrows connecting base forms to their past tense and present participle forms.
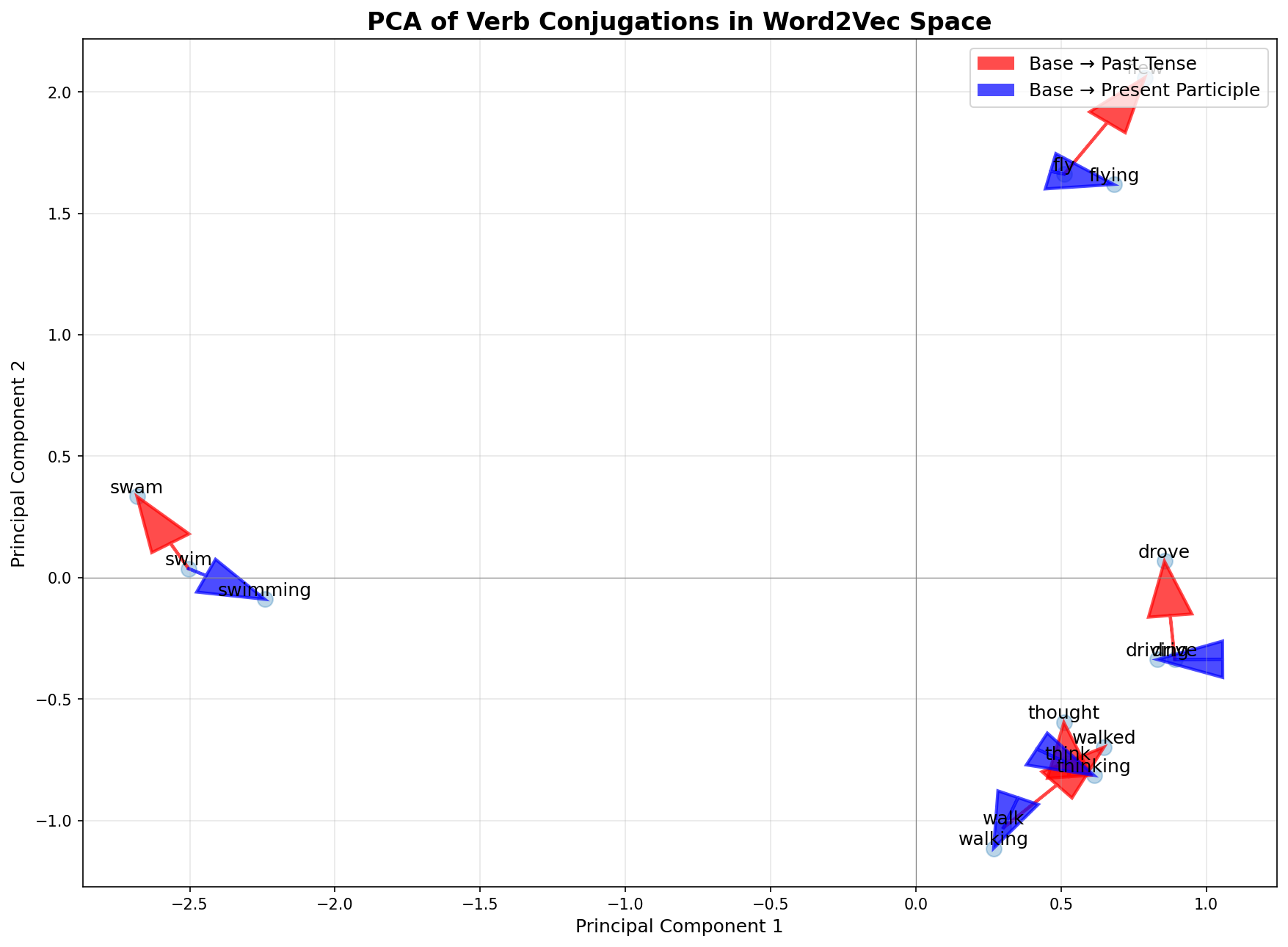
The visualization reveals strong consistency. The red arrows (base → past tense) point in a similar direction across different verbs, and the blue arrows (base → present participle) also show strong directional alignment but in a different direction. The first two principal components capture 44.33% of variance (PC1=27.54%, PC2=16.79%), indicating these tense transformations represent significant structural patterns in the embedding space.
This provides powerful visual evidence that grammatical transformations correspond to consistent vector offsets in Word2Vec. The parallelism isn't perfect (reflecting noise and complexities in language statistics), but the dominant trend is unmistakable.
Understanding Local Structure with t-SNE
While PCA reveals global linear structure, t-SNE (t-distributed Stochastic Neighbor Embedding) offers a different perspective by preserving local neighborhood relationships. Unlike PCA, t-SNE is non-linear and doesn't preserve global geometry. Relative positions between distant clusters are meaningless. However, it excels at revealing how words cluster based on similarity.
The key question here: do verbs group by their lemma (semantic similarity) or by their grammatical function (tense)?
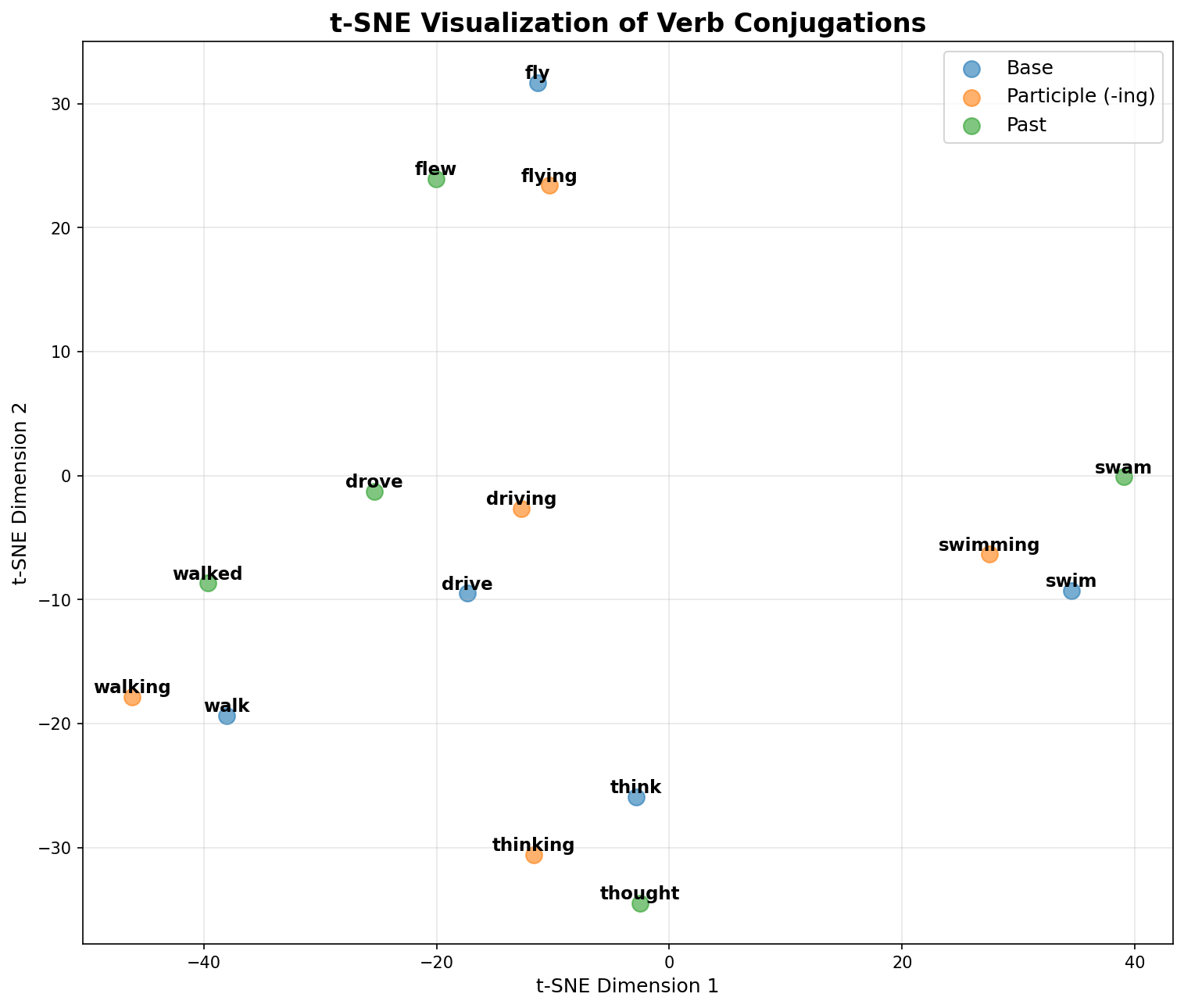
The t-SNE plot (using perplexity=5, optimized for our small dataset of 15 words) shows that lexical-semantic similarity (the lemma) is the dominant organizing force. All forms of "walk" cluster together, as do all forms of "swim." However, within these lemma-based clusters, there's subtle secondary structure. Past tense forms are consistently displaced from their base forms in loosely aligned directions.
This dual organization makes intuitive sense: "walked" is semantically closer to "walk" than to other past tense verbs, but it shares some abstract grammatical property with "swam" and "thought" that pulls it slightly in a shared direction.
The Contextual Shift: Why BERT Changes Everything
The advent of Transformer-based models like BERT marked a paradigm shift. Unlike Word2Vec's static embeddings (one fixed vector per word), BERT generates dynamic, contextual embeddings, a unique vector for each word token in each specific sentence.
Consider the word "bank." In Word2Vec, "bank" has a single vector that conflates its meanings (financial institution vs. river edge). This averaging inevitably loses precision. BERT solves this through its self-attention mechanism, which allows each word to "look at" all other words in a sentence when constructing its representation. In "I withdrew money from the bank," BERT's vector for "bank" will be geometrically close to "money," "account," and "withdraw." In "I sat on the river bank," the same word gets a completely different vector close to "river," "water," and "shore."
This contextuality fundamentally breaks the simple vector arithmetic that gave rise to the "tense axis" hypothesis. The analogy vector(A) - vector(B) + vector(C) requires single, static vectors for word types A, B, and C. In BERT, there's no single vector('walk') to subtract from vector('walked'). Each instance has a different vector depending on its sentence.
If grammatical information like tense is encoded in BERT, it must be represented as a more complex, context-dependent transformation within the space. The geometric transformation mapping "walk" to "walked" might differ in "He walked home" versus "The path was walked by many." The model likely learns a non-linear function that applies the concept of "past tense" to a verb's representation within its specific semantic and syntactic environment.
Despite this loss of simple linear structure, probing studies show that BERT's representations are even richer in linguistic information than static embeddings. BERT significantly outperforms Word2Vec on the same probing tasks, capturing nuances of syntax and semantics that static models miss. This creates a fascinating trade-off: we've sacrificed simple interpretability for massive gains in representational power.
Analysis of BERT's layers reveals a hierarchical processing structure: lower layers capture surface-level features like word morphology, middle layers encode local syntactic information like part-of-speech tags, and higher layers capture complex, long-range semantic relationships. This mirrors the classical NLP pipeline, emerging spontaneously from end-to-end training.
Synthesis: Does a "Tense Axis" Truly Exist?
After examining theoretical foundations, reviewing scientific literature, and conducting hands-on experiments, we can now provide a nuanced answer, one that depends on which type of embedding model we're discussing.
For static embeddings (Word2Vec/GloVe): A qualified "yes."
The term "axis" in the strict geometric sense (a single, clean, orthogonal dimension) is an oversimplification of high-dimensional space. However, the evidence strongly supports the existence of consistent and predictable directional offsets for grammatical transformations. The analogy experiments, PCA visualization showing parallel vectors, and the geometric reality of these offsets confirm that a "tense vector" is more than a metaphor. It's a tangible property of these embedding spaces.
Therefore, while "tense axis" may be slightly imprecise language, the terms "tense vector" or "tense offset" accurately describe a real, measurable phenomenon in static word embeddings.
For contextual embeddings (BERT): "No, not in any simple, global sense."
BERT's architecture precludes the existence of single, static vectors for words, invalidating the simple arithmetic underlying the "tense axis" hypothesis. While rigorous probing studies have definitively shown that tense information is robustly encoded and linearly decodable from BERT's representations, this information isn't accessible via a simple, global vector offset. The representation of tense is inextricably entangled with the semantic and syntactic context of the entire sentence.
Rather than adding a single "past tense vector" to a base verb, BERT applies a complex, context-dependent computational process that transforms the verb's representation based on its surrounding linguistic environment.
The Evolution of Our Understanding
This investigation highlights how our mental models of AI systems must evolve alongside the technology. The "tense axis" was a powerful and elegant abstraction that emerged from Word2Vec's surprisingly linear structure. It provided an intuitive mental model that drove foundational interpretability research.
However, as models have grown in complexity and capability, this simple mental model has become a geometric falsehood. Modern LLMs like BERT represent a fundamental trade-off: we've exchanged simple interpretability for massive gains in representational power and performance. The true nature of linguistic representation in these models likely isn't a set of fixed directions corresponding to human-defined grammatical categories, but rather a collection of complex, non-linear transformations learned by deep networks.
The field of NLP interpretability is thus moving beyond asking what information is stored in embeddings and toward understanding how that information is computationally processed and transformed. Future work will require more sophisticated tools for analyzing Transformer architectures, tracing the flow of linguistic information through attention heads and feed-forward layers, and ultimately moving from static geometric analysis to a dynamic, computational understanding of how models represent language.
A Note on Bias and Limitations
It's essential to acknowledge that any structure learned by these models, including the apparent tense vectors in Word2Vec, is a direct reflection of statistical patterns in the training data. These representations inherit the biases, stereotypes, and idiosyncrasies of the text corpora on which they're trained. The consistency of a "tense vector" is only as good as the consistency of tense usage in the training data. If certain verb forms are used inconsistently or in overlapping contexts, the resulting geometric structure will be noisier and less reliable.
Your Turn: Exploring Further
If you're intrigued by these geometric patterns in language models, consider these explorations:
- Compare embeddings: Run the same PCA analysis on GloVe vectors. Do you see similar parallel structure?
- Irregular verbs: Analyze whether irregular verbs (
sing/sang,think/thought) show tighter or looser parallel structure than regular verbs. - Cross-lingual analysis: Do multilingual models develop language-specific "tense axes" or shared cross-lingual grammatical structures?
- 3D visualization: Extend the PCA analysis to three dimensions using interactive tools like Plotly to explore additional variance.
The code and visualizations from this investigation are available in the research repository. All experiments use Poetry for dependency management, ensuring you can reproduce the results on your own machine.
While the elegant "tense axis" of the Word2Vec era may be a relic of simpler models, the fundamental inquiry it represents, the search for meaningful, interpretable structure in the latent spaces of language models, remains more relevant than ever. As you explore these embedding spaces yourself, you're participating in the ongoing project of understanding how artificial systems learn to represent the rich, structured complexity of human language.