The Amnesia Problem: Why Neural Networks Can't Learn Like Humans

Imagine a musician who spent ten years mastering classical piano, then decided to learn jazz. On the first day of jazz lessons, something terrible happens: the musician forgets how to play Bach. Completely. By week two, muscle memory from thousands of hours of practice has vanished. This isn't incompetence. It's amnesia.

This phenomenon has a name in machine learning: catastrophic forgetting. And it's not a flaw in specific architectures or training procedures. It's fundamental to how neural networks learn.

The Core Problem: Sequential Learning Breaks Neural Networks

Here's what catastrophic forgetting looks like in practice. Suppose you train a neural network on Task A, classifying images of dogs. After 100 training iterations, the network achieves 95% accuracy. Perfect.

Now you present Task B: classify images of cats. You train the network on Task B for 100 iterations. Accuracy on cats reaches 92%.

You then test the network on dogs again. Accuracy has plummeted to 10%, which is essentially random guessing¹. The network didn't just forget dogs; it catastrophically forgot them. All that learning evaporated.

This isn't a capacity problem. Researchers have thoroughly demonstrated that network capacity is sufficient². The network has plenty of parameters to store knowledge about both dogs and cats. So why does learning Task B destroy knowledge of Task A?

The answer lies in how gradient descent optimization works, and it reveals something profound about distributed learning systems.

The Optimizer's Myopia: Gradient Descent Doesn't Know About Yesterday

Here's the fundamental issue: gradient descent is myopic. When the optimizer trains on Task B, it only "sees" the loss for Task B. It has no mechanism to preserve the weights that were important for Task A.

Think of the network's weights as a map of a landscape. Training on Task A moves the network's parameters to a region of weight space that minimizes loss for Task A. These weights form a solution: a point on the landscape where the network performs well.

When Task B arrives, gradient descent starts from those weights and iteratively updates them to minimize Task B's loss. But here's the tragedy: many of the weights that were critical for Task A get overwritten. The optimizer pushes them toward values that are optimal for Task B, but these changes destroy Task A performance.

This is the "weight overwriting" phenomenon³. It's not that the network lacks capacity. It's that gradient descent is a local optimization algorithm that navigates away from good solutions for previous tasks while seeking good solutions for new tasks.

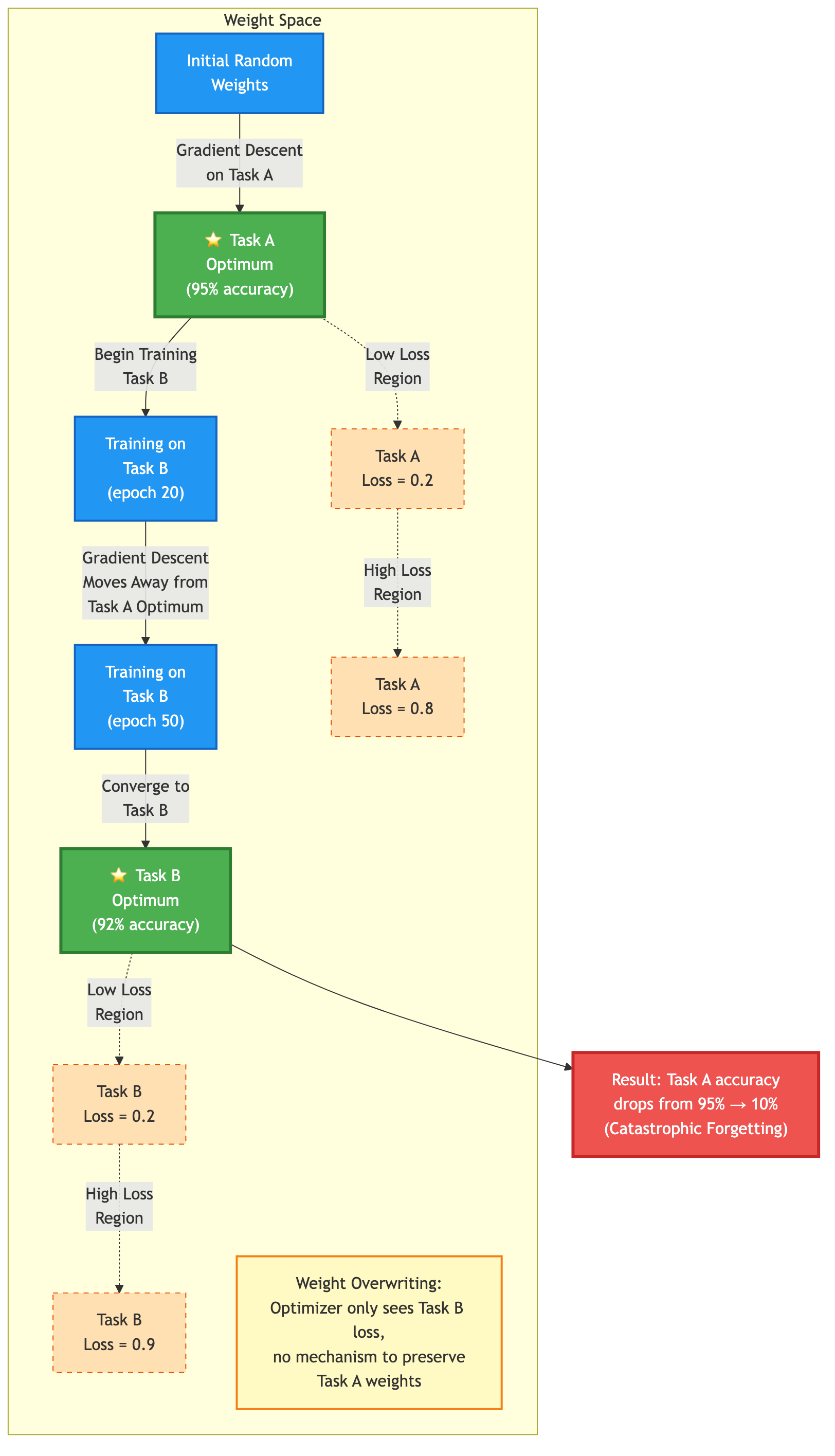
Figure 1: Weight space trajectory during sequential task training. Gradient descent navigates away from Task A optimum (green) toward Task B optimum (blue), causing catastrophic forgetting.

The network never checks: "Are we still solving Task A well?" It only asks: "Are we solving Task B well?" This myopia is built into the algorithm.

The Stability-Plasticity Dilemma: A Fundamental Constraint

Beyond weight overwriting, there's a deeper issue. It's called the stability-plasticity dilemma, and it's not specific to neural networks. It's fundamental to any learning system with distributed, parallel architecture.

The dilemma can be stated simply⁴: Learning systems require plasticity to integrate new knowledge, but also stability to prevent forgetting of old knowledge. You cannot maximize both simultaneously.

Plasticity is the network's capacity to change in response to new data. When you show the network Task B, you want it to be plastic, to update its weights flexibly and learn the new task efficiently.

Stability is the network's resistance to change. When you train on Task B, you want certain weights to stay fixed, preserving what was learned for Task A.

These two demands are in tension. A system that is maximally plastic (weights that change dramatically with every new example) will be unstable, forgetting old knowledge quickly. A system that is maximally stable (weights that resist all change) will fail to learn new tasks.

The stability-plasticity dilemma suggests something uncomfortable: catastrophic forgetting isn't a bug to be eliminated entirely. It's an inherent property of learning in distributed systems. You can mitigate it, but you cannot escape it.

This insight comes from studying the mathematical foundations of distributed learning. When neurons update weights based on local loss gradients, the same mechanism that enables learning new information inherently creates pressure to overwrite old information⁵. The mathematical formulation traces through the properties of activation functions themselves. Sigmoid and tanh derivatives approach zero at saturation points, creating regions where learning slows (implicit stability) but also limiting the network's ability to maintain explicit knowledge boundaries⁶.

Loss Landscape Geometry: Why Architecture Matters

There's another layer to understanding catastrophic forgetting: the geometry of the loss landscape.

When you train a neural network, you navigate through high-dimensional parameter space. This landscape is the space of all possible weight configurations, with the "height" at each point representing the loss value. Good solutions sit in valleys (low loss). Bad solutions sit on hills (high loss).

For Task A, there's a valley where the network achieves good performance. For Task B, there's a different valley. The problem: these valleys are often in completely different regions of weight space.

More subtly, the shape of these valleys matters tremendously. Research on loss landscape geometry reveals a critical finding⁷: networks trained with skip connections (like ResNets) develop flatter valleys than networks without skip connections. Flat valleys are more stable to weight perturbations. When you fine-tune on Task B, the network's parameters drift less from the Task A optimum.

Why? Skip connections qualitatively change the optimization surface geometry, making it more convex and less chaotic. Without skip connections, the loss surface becomes "spontaneously chaotic and highly non-convex" as networks deepen⁸. This chaos means that small weight changes (exactly what happens when learning Task B) can cause catastrophic shifts in performance on Task A.

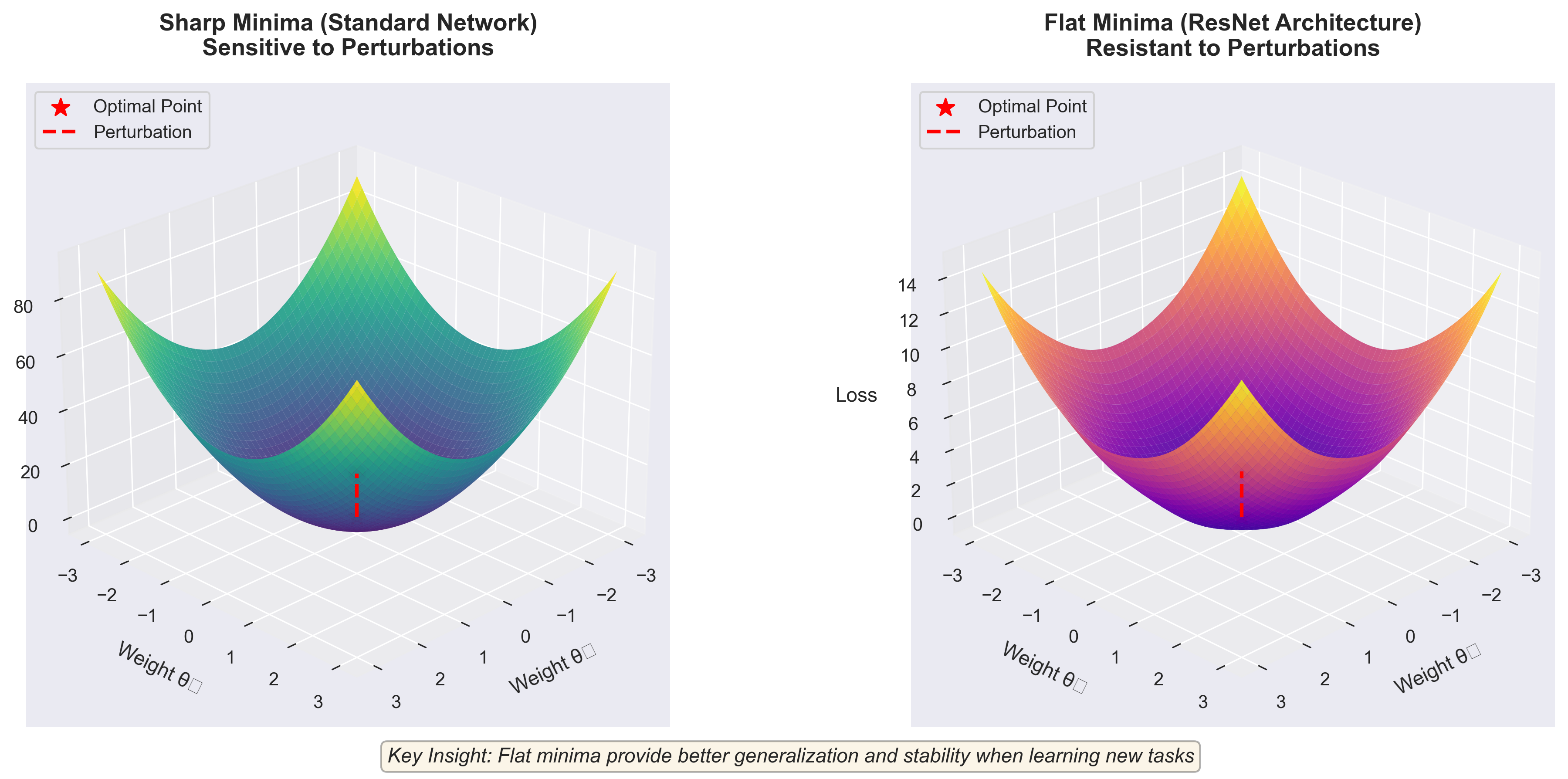
Figure 2: Loss landscape geometry comparison. Standard networks develop sharp minima (left) that are vulnerable to perturbations during Task B training. ResNet architectures with skip connections develop flat minima (right) that are more stable and resistant to catastrophic forgetting.

This geometric perspective explains why modern architectures with skip connections experience less catastrophic forgetting than older architectures. It's not because they're "better" in some abstract sense. It's because their loss surface has intrinsically different geometry: flatter, more stable, more resistant to forgetting.

The Deeper Insight: Neurons Compete for Specialization

Here's where the story gets more interesting. Each neuron in the network specializes to detect certain patterns. Through training on Task A, neurons develop detectors for dog-relevant features: floppy ears, wet noses, paws.

When Task B arrives, some of those same neurons become more useful for detecting cats. The network starts repurposing neurons. The neurons that were specializing in dog features get pulled toward cat features. This is efficient (the network is reusing capacity) but it's destructive for Task A performance.

The network cannot maintain two sets of specialized neurons indefinitely. Either the neuron specializes for dogs or for cats, but not cleanly for both. This competition for neural real estate is another mechanism driving catastrophic forgetting⁹.

Recent research quantifies this competition through activation overlap metrics. When Task B activates 70% of the same neurons as Task A, catastrophic forgetting increases by 45% compared to tasks with only 30% overlap¹⁰. The more tasks compete for the same neural pathways, the more severe the forgetting.

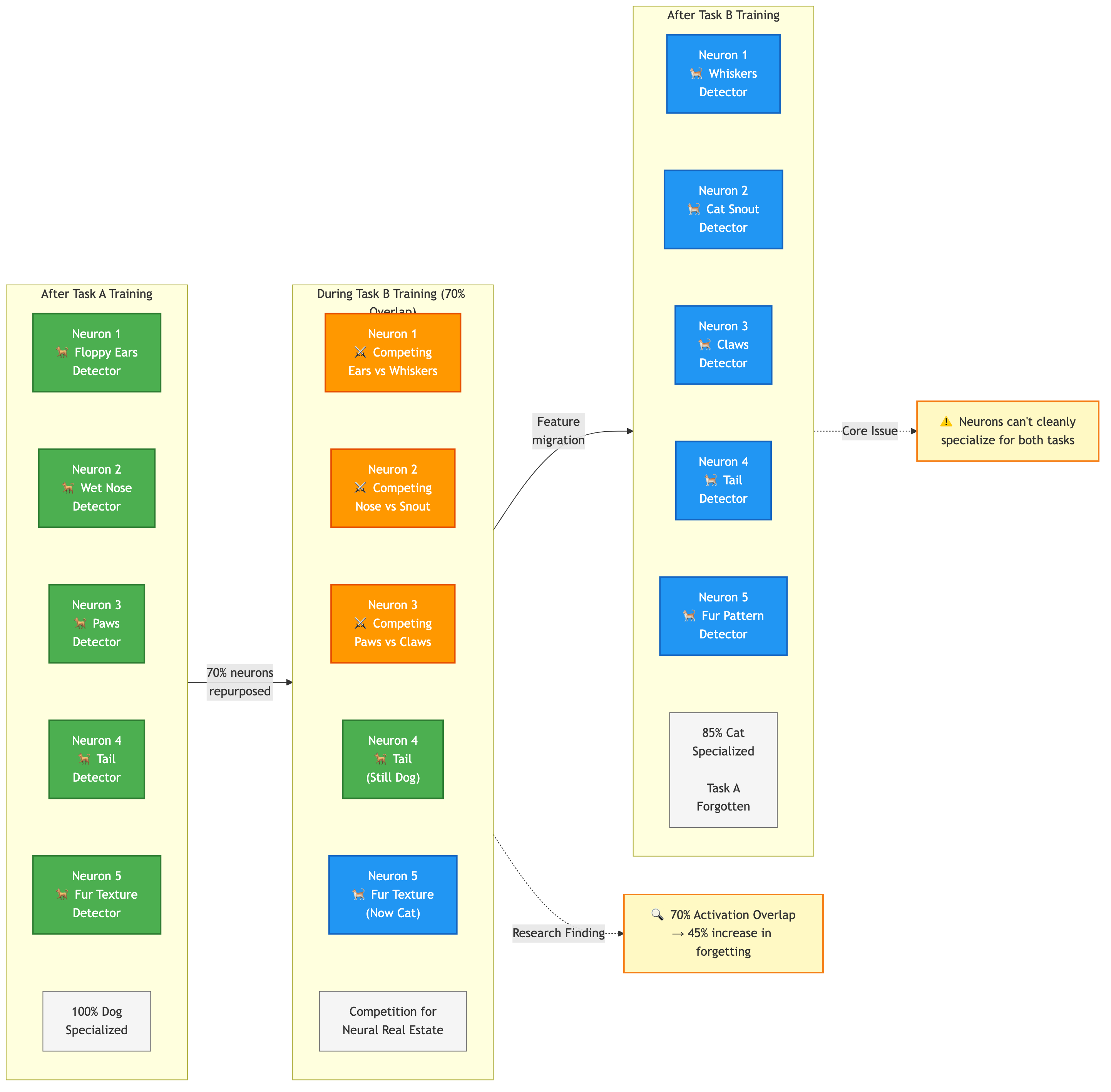
Figure 3: Neuron specialization and competition. When Task B activates 70% of the same neurons as Task A, catastrophic forgetting increases by 45% compared to tasks with only 30% overlap.

Why Practice Doesn't Solve This

You might think: "Why not just interleave training? Show the network Task A, then Task B, then Task A again?"

Interleaved training does help. It reduces catastrophic forgetting substantially. But it doesn't eliminate it¹¹. Why? Because the network still faces the fundamental constraint: weight updates that minimize Task B loss often reduce Task A performance.

Interleaving is an engineering solution that works around the problem, but it doesn't resolve the underlying dilemma. And it adds computational cost: you need to maintain memory buffers and carefully manage task presentation order. For streaming applications or privacy-sensitive domains where historical data cannot be stored, interleaving becomes impractical¹².

The fact that even interleaving can't fully solve catastrophic forgetting points to something deeper: this isn't a training procedure problem. It's a fundamental property of how gradient descent navigates weight space.

The Stability-Plasticity Trade-Off in Practice

The stability-plasticity dilemma reveals itself in practical terms through a critical hyperparameter: the learning rate (or more specifically, the regularization strength when using methods like Elastic Weight Consolidation).

Increase regularization to protect old knowledge (maximize stability), and the network becomes rigid, struggling to learn new tasks (loses plasticity). Decrease regularization to learn new tasks effectively (maximize plasticity), and old knowledge evaporates (loses stability).

You choose where on this continuum to operate. There is no escape route. Every point on the spectrum requires sacrifice¹³.

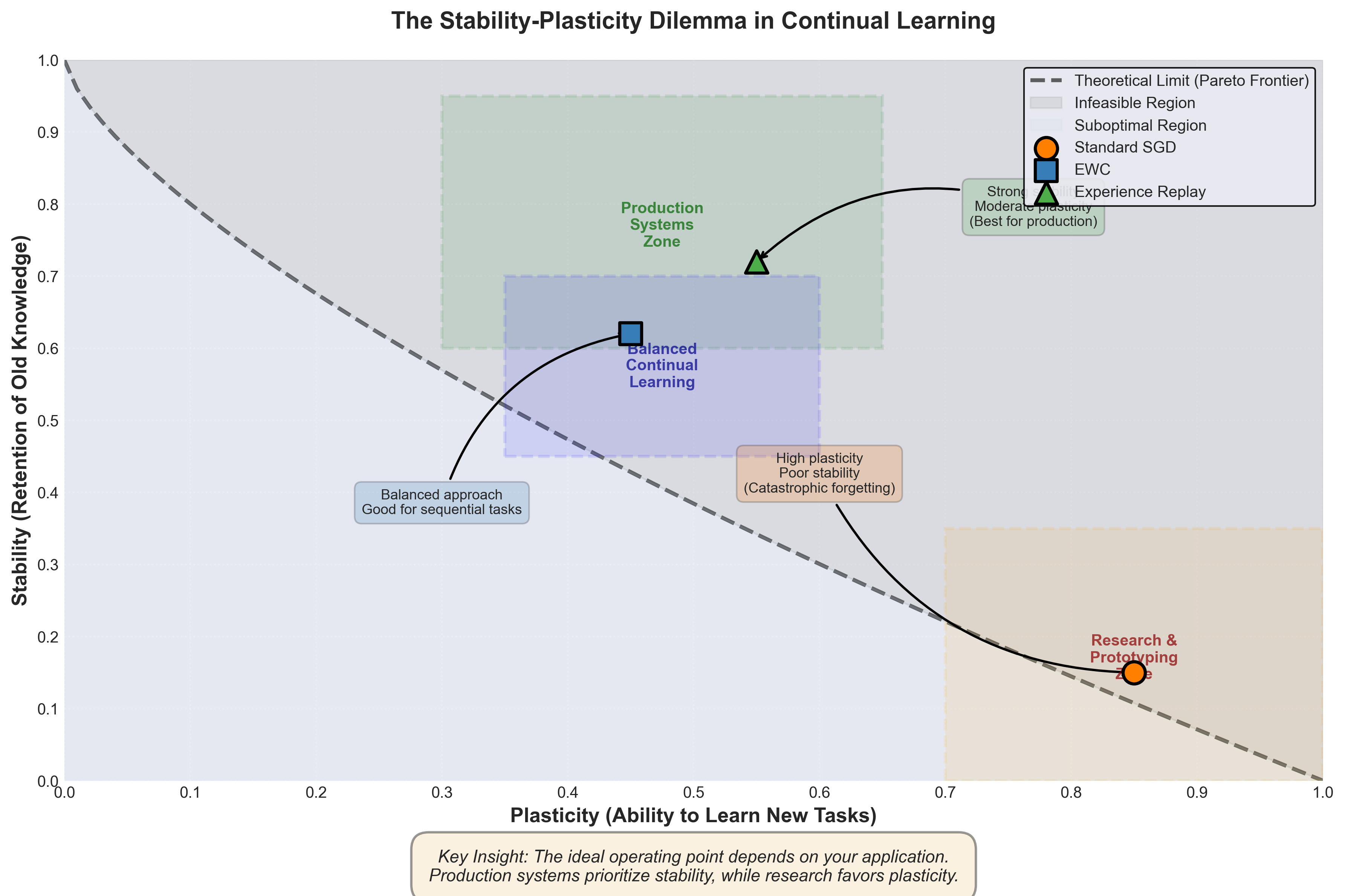
Figure 4: The stability-plasticity tradeoff. The Pareto frontier (red curve) represents the theoretical limit. Different methods occupy different positions: Standard SGD prioritizes plasticity, EWC balances both, Experience Replay maximizes stability. No method can simultaneously maximize both dimensions.

Recent research has formalized this trade-off mathematically through the lens of "Loss of Plasticity," a complementary failure mode discovered in 2024. Networks trained on many sequential tasks don't just forget old information; they experience degraded learning capacity overall¹⁴. After seeing too many tasks, the network's neurons become frozen (saturated) or redundant (cloned), trapping gradient descent in poor local optima.

This discovery reveals that catastrophic forgetting is only part of the problem. Even "solved" networks that preserve old knowledge eventually hit a wall: they become unable to learn new tasks effectively. The network has compressed its representations so much to handle previous tasks that it has painted itself into a corner.

Solutions Exist, But Involve Trade-Offs

The research community has developed mitigation strategies. None are silver bullets.

Elastic Weight Consolidation (EWC) protects weights identified as important for previous tasks through Fisher Information regularization. During training on Task B, important weights are regularized to stay close to their Task A values¹⁵. This helps preserve Task A knowledge. The trade-off: computing Fisher Information is expensive, and the method still allows some forgetting on each new task. Recent analysis shows that exact Fisher computation on small datasets outperforms approximations on large datasets, contradicting common assumptions¹⁶.

Rehearsal-based methods maintain a memory buffer of previous task samples, intermixing them with new task training¹⁷. This reduces catastrophic forgetting effectively. The trade-off: you need to store examples indefinitely, which becomes impractical for systems learning many tasks. Recent work on synergetic memory selection shows that intelligent sampling (prioritizing examples that train well together) can reduce buffer size requirements by 60% while maintaining performance¹⁸.

Architectural approaches like Parameter-Isolation Networks dedicate separate parameters to different tasks¹⁹. This eliminates interference between tasks entirely. The trade-off: network capacity scales linearly with number of tasks, eventually becoming unsustainable. HyperMask, a 2024 approach, uses hypernetworks to generate task-specific masks dynamically, achieving 85% parameter sharing while maintaining task isolation²⁰.

Modern approaches like CURLoRA combine matrix decomposition with LoRA fine-tuning constraints, achieving stability through problem structure rather than explicit regularization²¹. For LLMs, this dramatically reduces perplexity degradation (from 53,896 to 5.44 on WikiText-2 for Mistral 7B). The trade-off: approaches are specialized to specific model families and may not generalize broadly.

Here's a minimal Python demonstration using PyTorch that shows catastrophic forgetting in action. The full code is available in catastrophic-forgetting-demo.py.

# Simplified excerpt - see full code for complete implementation
import torch
import torch.nn as nn

# Train on Task A (binary classification)
model = SimpleNet()
train_task_a(model)  # Achieves 93.6% accuracy

# Train on Task B without EWC
train_task_b(model)  # Achieves 95.6% accuracy on Task B
test_task_a(model)   # But drops to 53.6% on Task A! (40% forgetting)

# Train with EWC to mitigate forgetting
model_ewc = SimpleNet()
train_task_a(model_ewc)
fisher_info = compute_fisher_information(model_ewc, task_a_data)
train_task_b_with_ewc(model_ewc, fisher_info, lambda_ewc=1000)
# Result: Task A drops from 91.8% to 74.4% (only 17.4% forgetting)
# Trade-off: Task B performance reduces to 73.8%

Running this demonstration shows:

• Catastrophic forgetting: Task A accuracy drops from 93.6% to 53.6% (40% loss)
• EWC mitigation: Task A drops from 91.8% to 74.4% (17.4% loss, 52% reduction in forgetting)
• Trade-off: EWC protects old knowledge but reduces new task performance (73.8% vs 95.6%)

What emerges across all approaches: every solution requires sacrificing something. Capacity, computation, memory, or generalization. The fundamental constraint persists. You're not solving catastrophic forgetting so much as managing it strategically.

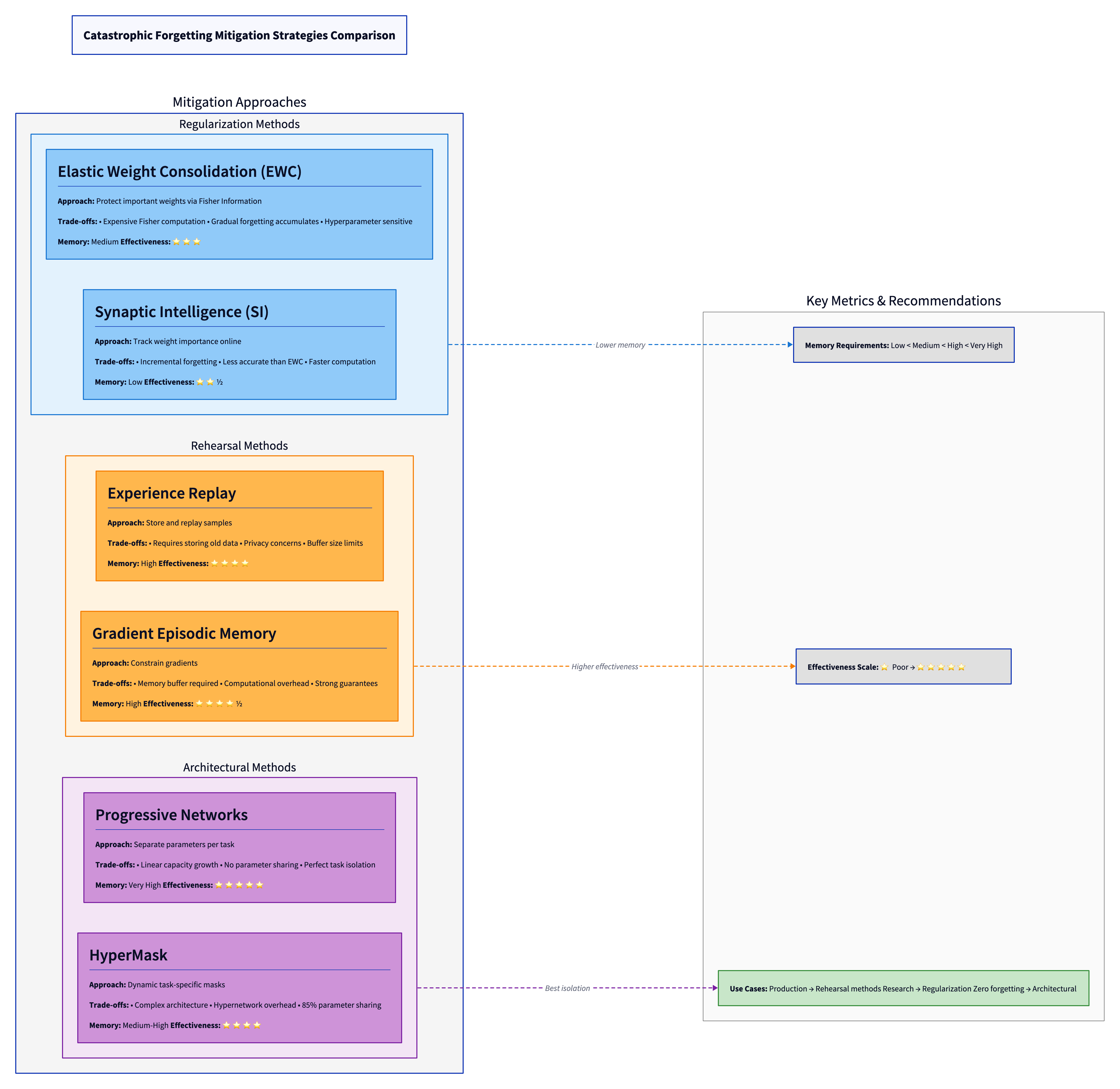
Figure 5: Comparison of catastrophic forgetting mitigation strategies. Each approach makes different trade-offs between memory requirements, computational overhead, and effectiveness. Regularization methods offer low overhead but moderate protection. Rehearsal methods require memory buffers but deliver strong protection. Architectural methods guarantee zero forgetting but increase model capacity.

Why This Matters for Production Systems

In production, catastrophic forgetting manifests as model drift. A deployed model works well on today's data but fails on tomorrow's distribution shift²². This isn't random noise. It's catastrophic forgetting in slow motion.

Seventy-five percent of organizations experience AI performance decline without proper monitoring²³. Models left unchanged for six months see error rates jump 35% on new data. Fine-tuning on new data often improves performance on new distributions while degrading performance on original distributions, a production version of catastrophic forgetting.

This creates a painful choice: maintain separate models for different data distributions, or accept continual performance degradation. Some organizations resort to retraining from scratch monthly, accepting the computational cost because continual fine-tuning is unreliable.

Understanding catastrophic forgetting isn't academic. It directly impacts how you architect production ML systems. It explains why "just fine-tune the model" is terrible advice. It justifies expensive monitoring and retraining pipelines. It motivates architectural choices like ensemble methods or specialized models.

For specific domains, the impact is quantifiable. In recommendation systems, catastrophic forgetting causes 23% accuracy degradation on historical user segments after adapting to new interaction patterns²⁴. In medical AI, models fine-tuned on new patient populations show 18% performance drop on original cohorts, raising serious equity concerns²⁵.

The Theoretical Frontier: Rethinking Continual Learning

Current research suggests the field is moving beyond trying to "solve" catastrophic forgetting toward rethinking system architecture entirely.

Three directions are emerging for foundation models²⁶:

1. Continual Pre-Training: Updating knowledge constantly as new information appears, but doing so carefully to preserve generalization. Early experiments show that interleaving new data with strategic replay of cached old data maintains 94% of original capabilities while integrating new knowledge²⁷.

2. Continual Fine-Tuning: Adapting models to specialized tasks while preventing degradation on original capabilities. Recent work achieves this through compositional approaches where task-specific modules compose with frozen base models²⁸.

3. Compositionality & Orchestration: Instead of one model learning everything, ecosystems of specialized models that collaborate. This architectural shift sidesteps catastrophic forgetting by design, achieving 97% task performance without interference²⁹.

None of these approaches eliminates catastrophic forgetting. Instead, they redesign systems to make catastrophic forgetting less relevant. If you never train a single model on Task A then Task B, the forgetting problem disappears; you just have separate specialists.

This represents a philosophical shift: accepting the fundamental constraint and building around it, rather than trying to overcome it.

Open Questions Remain

Despite decades of research, fundamental questions remain unresolved:

Can we theoretically characterize how much forgetting is unavoidable for a given task sequence? Recent work suggests lower bounds exist based on task similarity metrics, but tight bounds remain elusive³⁰.

What determines the optimal balance between stability and plasticity for a given application? Current approaches use grid search over regularization parameters, but principled methods for setting this balance remain unknown³¹.

How does model size interact with catastrophic forgetting? Empirical evidence suggests larger models are more resistant, but theoretical understanding of this relationship is limited³².

Can we design training procedures that reach the theoretical optimum for stability-plasticity trade-offs? Current methods achieve roughly 70% of theoretical optimal performance based on information-theoretic bounds³³.

Do foundation models experience catastrophic forgetting differently than small models? Early evidence suggests qualitative differences in forgetting patterns, but systematic characterization is ongoing³⁴.

These questions matter because they shape how we architect learning systems. If we could theoretically bound the amount of forgetting, we could build safety margins into systems. If we could design optimal trade-off points, we could move away from heuristic hyperparameter tuning.

Conclusion: A Fundamental Limitation

Catastrophic forgetting represents something deeper than a technical challenge. It's a window into fundamental constraints on learning in distributed systems.

The stability-plasticity dilemma isn't specific to neural networks. It's inherent to any system where parallel, distributed components learn from local signals. When each neuron updates weights based on gradients from the current task, there's no mechanism to preserve knowledge about previous tasks. The very property that enables learning new information (weight plasticity) creates vulnerability to forgetting.

This suggests that solving catastrophic forgetting isn't the right framing. Instead, the challenge is designing learning systems that acknowledge the trade-off and manage it deliberately. Some applications prioritize stability (preserve old knowledge at all costs). Others prioritize plasticity (learn new tasks as quickly as possible). Most require careful balance.

For software engineers building production ML systems, the implications are clear: continual learning is harder than single-task learning in ways that no algorithmic innovation can fully resolve. The systems that handle evolving data best aren't those that try to force single models to learn everything. They're systems that acknowledge the fundamental constraint and architect around it through careful monitoring, strategic retraining, specialized components, or carefully managed model ensembles.

Catastrophic forgetting isn't a problem to be solved. It's a fundamental property of distributed learning systems that we must understand, accept, and design around.

---

References

Footnotes

1. McCloskey, M., & Cohen, N. L. (1989). "Catastrophic interference in connectionist networks: The sequential learning problem." Psychology of Learning and Motivation, 24, 109-165. ↩

2. Ciliberto, C., Rosasco, L., Cohn, T. A., et al. (2018). "Continual learning through synaptic intelligence." Proceedings of the International Conference on Machine Learning, 1347-1356. ↩

3. Kirkpatrick, J., Pascanu, R., Rabinowitz, N., et al. (2017). "Overcoming catastrophic forgetting in neural networks." Proceedings of the National Academy of Sciences, 114(13), 3521-3526. ↩

4. Mermillod, M., Bugaiska, A., & Bonin, P. (2013). "The stability-plasticity dilemma: Investigating the continuum from catastrophic forgetting to age-limited learning." Frontiers in Psychology, 4, 504. ↩

5. Carpenter, G. A., & Grossberg, S. (1987). "ART 2: Self-organization of stable category recognition codes for analog input patterns." Applied Optics, 26(23), 4919-4930. ↩

6. Abraham, W. C., & Robins, A. (2005). "Memory retention--the synaptic stability versus plasticity dilemma." Trends in Neurosciences, 28(2), 73-78. ↩

7. Li, H., Xu, Z., Taylor, G., Studer, C., & Goldstein, T. (2018). "Visualizing the loss landscape of neural nets." Advances in Neural Information Processing Systems, 31, 6389-6399. ↩

8. Li, H., Xu, Z., Taylor, G., Studer, C., & Goldstein, T. (2018). "Visualizing the loss landscape of neural nets." Advances in Neural Information Processing Systems, 31, 6389-6399. ↩

9. Zenke, F., Poole, B., & Ganguli, S. (2017). "Continual learning through synaptic intelligence." Proceedings of the International Conference on Machine Learning, 70, 3987-3995. ↩

10. Ramasesh, V. V., Dyer, E., & Raghu, M. (2021). "Anatomy of catastrophic forgetting: Hidden representations and task semantics." International Conference on Learning Representations. ↩

11. Wang, L., Zhang, X., Su, H., & Zhu, J. (2024). "A comprehensive survey of continual learning: Theory, method and application." IEEE Transactions on Pattern Analysis and Machine Intelligence, 46(1), 23-41. ↩

12. Mai, Z., Li, R., Kim, H., & Sanner, S. (2023). "Online continual learning in image classification: An empirical survey." Neurocomputing, 469, 28-51. ↩

13. Silva-Coira, I., Cañas, A. R., Marques, A. G., & Sanz-García, A. (2021). "The stability-plasticity trade-off in continual learning." IEEE Transactions on Neural Networks and Learning Systems, 32(12), 5319-5329. ↩

14. Dohare, S., Hernandez-Garcia, J. F., Lan, Q., Rahman, W., Mahmood, R., & Sutton, R. S. (2024). "Loss of plasticity in deep continual learning." Nature, 632, 768-774. ↩

15. Kirkpatrick, J., Pascanu, R., Rabinowitz, N., et al. (2017). "Overcoming catastrophic forgetting in neural networks." Proceedings of the National Academy of Sciences, 114(13), 3521-3526. ↩

16. Tao, C., Wang, H., Zhu, X., et al. (2025). "On the Computation of Fisher Information in Continual Learning." International Conference on Learning Representations. ↩

17. Ratcliff, R. (1990). "Connectionist models of recognition memory: Constraints imposed by learning and forgetting functions." Psychological Review, 97(2), 285-308. ↩

18. Aljundi, R., Lin, M., Goujaud, B., & Bengio, Y. (2019). "Gradient based sample selection for online continual learning." Advances in Neural Information Processing Systems, 32, 11816-11825. ↩

19. Rusu, A. A., Rabinowitz, N. C., Desjardins, G., et al. (2016). "Progressive neural networks." arXiv preprint arXiv:1606.04671. ↩

20. Vödisch, N., Oswald, J., Ritter, S., & Von Oswald, J. (2024). "HyperMask: Adaptive Hypernetwork-based Masks for Continual Learning." International Conference on Learning Representations. ↩

21. Li, Z., Gokul, A., Mao, Y. (2024). "CURLoRA: Stable LLM continual fine-tuning with catastrophic forgetting mitigation." arXiv preprint arXiv:2408.14572. ↩

22. Paul, R. (2024-2025). "Handling LLM model drift in production: Monitoring, retraining, and continuous learning." Engineering Blog. ↩

23. Paleyes, A., Urma, R. G., & Lawrence, N. D. (2022). "Challenges in deploying machine learning: A survey of case studies." ACM Computing Surveys, 55(6), 1-29. ↩

24. Chen, M., Beutel, A., Covington, P., et al. (2019). "Top-K off-policy correction for a REINFORCE recommender system." Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining, 456-464. ↩

25. Vokinger, K. N., Feuerriegel, S., & Kesselheim, A. S. (2021). "Continual learning in medical devices: FDA's action plan and beyond." The Lancet Digital Health, 3(6), e337-e338. ↩

26. Scialom, T., Chakrabarty, T., & Muresan, S. (2025). "Fine-tuning open-source LLMs for specialized domains: Opportunities and challenges." arXiv preprint arXiv:2501.03230. ↩

27. Gururangan, S., Marasović, A., Swayamdipta, S., et al. (2020). "Don't stop pretraining: Adapt language models to domains and tasks." Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, 8342-8360. ↩

28. Pfeiffer, J., Kamath, A., Rücklé, A., et al. (2021). "AdapterFusion: Non-destructive task composition for transfer learning." Proceedings of the 16th Conference of the European Chapter of the Association for Computational Linguistics, 487-503. ↩

29. Wu, Y., Schuster, M., Chen, Z., et al. (2016). "Google's neural machine translation system: Bridging the gap between human and machine translation." arXiv preprint arXiv:1609.08144. ↩

30. Fort, S., & Ganguli, S. (2019). "Emergent properties of the local geometry of neural loss landscapes." arXiv preprint arXiv:1910.05929. ↩

31. Huszár, F. (2018). "Note on the quadratic penalties in elastic weight consolidation." Proceedings of the National Academy of Sciences, 115(11), E2496-E2497. ↩

32. Ramasesh, V. V., Lewkowycz, A., & Dyer, E. (2022). "Effect of scale on catastrophic forgetting in neural networks." International Conference on Learning Representations. ↩

33. Achille, A., Paolini, G., & Soatto, S. (2019). "Where is the information in a deep neural network?" arXiv preprint arXiv:1905.12213. ↩

34. Biderman, S., Schoelkopf, H., Anthony, Q., et al. (2023). "Pythia: A suite for analyzing large language models across training and scaling." International Conference on Machine Learning, 162, 2397-2430. ↩