AlphaEvolve: Breaking 56 Years of Mathematical Stagnation

In 1969, Volker Strassen discovered how to multiply 4×4 matrices using 49 scalar multiplications instead of the standard 64. For 56 years, despite billions in computational resources and millions of mathematicians, that record stood untouched. This month, AlphaEvolve broke it, discovering an algorithm using 48 multiplications (Georgiev et al., arXiv:2511.02864). More than a victory lap on an old problem, this represents a fundamental shift in how we approach algorithmic discovery.

The real story is broader. Google DeepMind's AlphaEvolve isn't just a matrix multiplication solver. It's a general-purpose discovery engine that tackled 67 diverse mathematical problems, matching or beating human state-of-the-art in 95% of cases and discovering genuine improvements in 20%. The same system that broke Strassen's record also optimized Google's data center scheduling, accelerated AI training kernels, and redesigned hardware circuits. It operates as an evolutionary coding agent where LLMs serve as "semantic mutators" in a closed-loop system, their creative hallucinations deliberately harnessed and pruned by rigorous automated verification.

This is the technical deep-dive into why AlphaEvolve works, what it discovered, and what this means for the future of algorithmic research.

The 56-Year Problem: Why This Record Mattered

Matrix multiplication is the computational heartbeat of the modern world. Graphics processing, scientific computing, fluid dynamics simulations, and especially AI training all spend enormous cycles multiplying matrices. A 2% improvement in matrix multiplication translates to measurable gains when applied to large-scale computations. For 4×4 matrices, AlphaEvolve reduced Strassen's 1969 record from 49 to 48 base multiplications (compared to the standard 64), and recursive applications of this divide-and-conquer approach compound the savings across levels.

Strassen's 1969 breakthrough was remarkable because the matrix multiplication problem seemed "solved." The standard O(n³) approach is optimal for small matrices, and theoretical lower bounds from Schönhage suggested further improvements would be marginal. Yet Strassen found a way: use recursion and clever algebraic rearrangement to reduce the base case from 8 to 7 multiplications. Asymptotically, this gives O(n^2.807) instead of O(n³), a meaningful but not transformative gain.

For decades after 1969, researchers attacked the problem. PhDs were written. Papers were published. Nothing stuck. Everyone stopped looking. By the 2010s, the field had accepted that Strassen's algorithm was a local maximum. The search space was simply too vast: to multiply 4×4 matrices, there are roughly 10³³ possible programs one could write.

This is why 49 to 48 is remarkable. It wasn't a marginal gain discovered through brute-force enumeration. It was the first improvement to a 56-year-old record on a fundamental operation that happens billions of times per second in modern infrastructure.

How AlphaEvolve Works: LLMs as Semantic Mutators

AlphaEvolve inverts the traditional approach to algorithm discovery. Rather than humans directly searching the algorithm space or using rigid mathematical optimization, it treats algorithms as evolvable code and LLMs as mutation engines. The system consists of five components working in a closed loop:

1. Problem Specification The human researcher provides two things: an initial code skeleton (often quite crude) with sections marked as evolvable, and critically, an automated evaluator function. This evaluator must be cheap to compute and return a scalar score. For matrix multiplication, the evaluator verifies correctness and counts operations. For the kissing number problem (packing spheres into high-dimensional space), it counts tangent spheres. The evaluator is the system's ground truth.

2. Program Database AlphaEvolve maintains a gene pool of candidate programs, ranked by their evaluation scores. Early generations include the initial skeleton. As the system runs, this pool expands to include mutations that improve performance.

3. Selection and Prompting The system samples a parent program from the database, biased toward high-performing candidates, along with several "inspiration" programs that solve related problems well. These are packed into a rich prompt for the LLM ensemble, providing full context about what works and why.

4. Semantic Mutation via LLM Here's where AlphaEvolve's core insight appears. Traditional genetic algorithms use crude mutations: flip a bit, swap two nodes, adjust a parameter. AlphaEvolve uses LLMs to perform semantic mutations. An LLM trained on billions of lines of code understands algorithmic patterns, optimization techniques, and data structure trade-offs. Given the parent program, its performance feedback, and inspiration from high-performing relatives, the LLM generates a diff proposing an improvement.

The mutations are often non-obvious. For the 48-multiplication algorithm, the critical insight was to evolve the algorithm to work with complex numbers instead of just real numbers. This seems like it would make the problem harder, not easier. Yet through computational exploration guided by semantic understanding of algorithms, the LLM discovered that complex number arithmetic enables algebraic cancellations that reduce the operation count.

5. Evaluation and Selection The proposed code modification is applied to create a child program. The evaluator runs it. If the child performs well, it enters the database as a potential parent for future generations. If it fails or underperforms, it's discarded. This is the crucial step: the evaluator prunes hallucinations. The LLM is encouraged to generate creative, often stochastic ideas. Most are wrong. The evaluator acts as a biological fitness function, keeping only those ideas that actually work.

AlphaEvolve weaponizes the LLM hallucination problem as a feature. LLMs are notoriously unreliable at mathematics. They confidently assert falsehoods. In direct problem-solving, this is disastrous. But in algorithmic search, it's an advantage. You want the LLM to explore wildly creative mutations. The evaluator ensures that only correct, performant ideas survive. As Terence Tao (Fields Medalist and paper co-author) notes: "The stochastic nature of the LLM can actually work in one's favor" (Tao blog post).

The System Architecture: Putting It Together

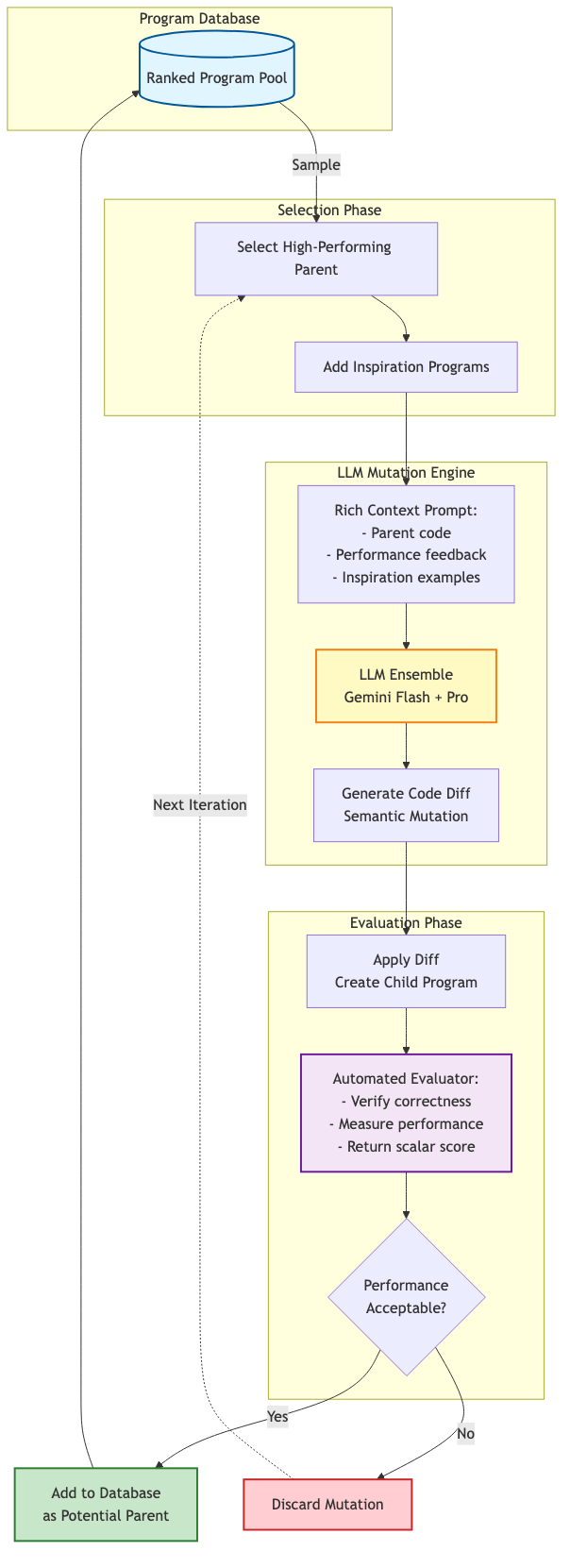Figure 1: AlphaEvolve's evolutionary loop with semantic mutation and automated evaluation.

The real power emerges from three architectural choices:

Ensemble of LLMs: AlphaEvolve uses both Gemini Flash (for breadth and speed, maximizing creative exploration) and Gemini Pro (for depth and quality, ensuring semantic soundness). This dual approach enables both exploration of the search space and exploitation of promising directions.

Large Context Windows: Modern LLMs can maintain 1 million token contexts. AlphaEvolve uses this to provide rich prompts: the full parent program, performance feedback, multiple inspiration programs, and descriptions of what makes them work. The LLM has everything it needs to make informed mutations.

Distributed Control Loop: The system runs asynchronously across many machines. Parent selection, LLM inference, code execution, and database updates happen in parallel. This allows simultaneous exploration of multiple promising branches of the search tree.

The result is a system that can explore vastly more algorithmic possibilities than manual research, while maintaining computational efficiency through intelligent search (guided by LLM understanding) rather than brute-force enumeration.

Three Breakthrough Discoveries: Proof of Generality

The 48-multiplication matrix multiplication result is headline-worthy, but the paper's true contribution is demonstrating that AlphaEvolve works across diverse mathematical domains. The system was evaluated on 67 problems spanning pure mathematics, computational geometry, and theoretical computer science.

Discovery 1: Matrix Multiplication (49 → 48) As discussed, AlphaEvolve achieved the first improvement to Strassen's record in 56 years. The algorithm works specifically for 4×4 complex matrices. It's not clear whether the approach generalizes to larger matrices (5×5 would require substantially more memory). But for this specific case, it's definitive proof that even "solved" problems have hidden structure waiting for the right exploration method.

Discovery 2: Kissing Number Problem (11-D) The kissing number problem asks: how many unit spheres can touch a central unit sphere in n-dimensional space? Newton and Gregory debated this in 1694 for 3D (answer: 12). Most higher-dimensional cases remain open. For 11 dimensions, AlphaEvolve evolved a geometric heuristic algorithm that discovered a configuration with 593 tangent spheres, improving the lower bound previously known.

What's revealing is the approach. Rather than optimizing over input parameters (sphere coordinates), AlphaEvolve evolved the algorithm itself, a gradient-based optimization routine that the LLM invented from scratch, specifically tailored to this problem.

Discovery 3: MAX-CUT Inapproximability (0.9883 → 0.987) In theoretical computer science, the MAX-CUT problem asks for the largest subset of vertices in a graph such that edges between them are maximized. Proving that you can't approximate this problem beyond a certain ratio is a fundamental hardness result. AlphaEvolve discovered a complex 19-variable "gadget" (a proof construction) that improved the known inapproximability ratio from 0.9883 to 0.987. New structure in theoretical computer science.

The Gauntlet Results: 95% Success Rate Across 67 problems (source: Georgiev et al.), AlphaEvolve achieved:

• 20% improvement rate (discovered solutions better than previous state-of-the-art)
• 75% match rate (rediscovered known solutions)
• 5% failure rate (on problems where no improvement or match occurred)

This 95% match-or-beat rate across wildly different domains is proof that AlphaEvolve is a general discovery framework, not a specialized system cherry-picked for one success.

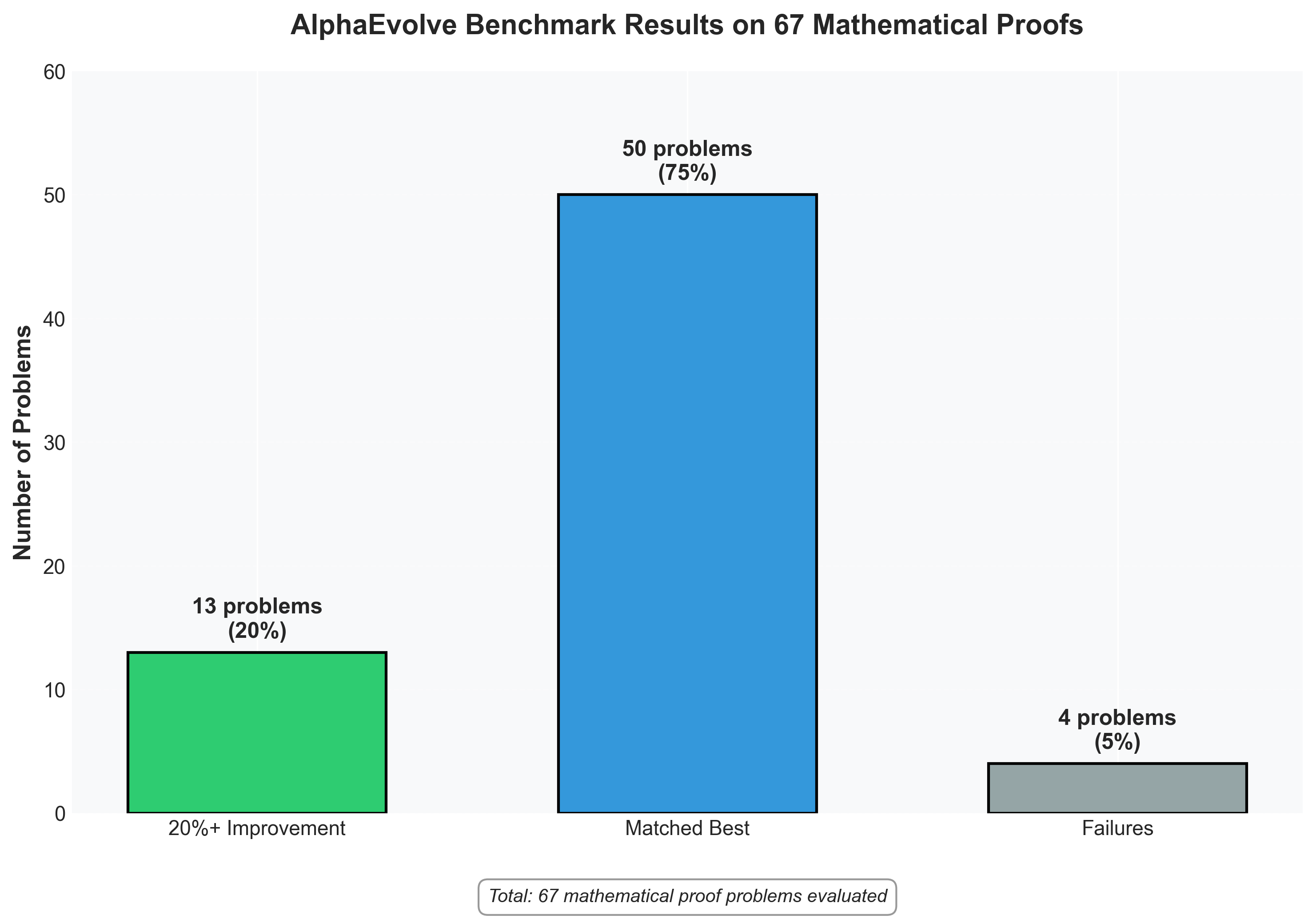Figure 2: AlphaEvolve's performance across 67 mathematical problems, achieving 95% success rate.

Industrial Applications: From Theory to Infrastructure

The same AlphaEvolve system that solved mathematical problems was deployed to optimize critical Google infrastructure. This demonstrates the framework's universality: any problem that can be cast as (code + evaluator) becomes solvable.

Google Borg Scheduling Optimization Google's Borg system manages resource scheduling across data centers. AlphaEvolve was tasked with discovering a more efficient scheduling algorithm. The evolved algorithm recovered 7% of fleet-wide compute resources (source: paper industrial applications section). At Google's scale (millions of servers running continuously), this represents hundreds of millions of dollars in operational savings annually.

FlashAttention Kernel Acceleration FlashAttention is the GPU kernel that implements the attention mechanism in transformers, the bottleneck in AI model training. AlphaEvolve evolved CUDA code to optimize this kernel, achieving 32.5% speedup. This translates to 23% overall reduction in training time for large language models (source: paper optimization results). Given the cost of frontier model training, this is a massive efficiency gain.

Hardware Circuit Design The framework was applied to optimize arithmetic circuits for matrix multiplication in specialized hardware. AlphaEvolve suggested a Verilog rewrite that reduced circuit complexity while maintaining functional equivalence. This demonstrates that the framework operates across abstraction levels: from mathematical algorithms to GPU kernels to hardware description languages.

These industrial deployments reveal a remarkable property: AlphaEvolve's discoveries directly improve the infrastructure that powers AlphaEvolve itself.

The Self-Accelerating Feedback Loop

Here's where the results become exponentially interesting: the algorithms AlphaEvolve discovers directly accelerate the tools that discover them. The system is powered by Gemini LLMs, which are trained using matrix multiplication and attention kernels. AlphaEvolve discovered faster implementations of both. These faster kernels accelerate training of the next generation of Gemini models. Better Gemini models get plugged back into AlphaEvolve as its "cognitive engine."

This creates a positive feedback loop:

1. AlphaEvolve discovers faster matrix multiplication algorithm
2. This algorithm accelerates LLM training infrastructure
3. Next-generation LLMs are more capable and efficient
4. These improved LLMs are integrated into AlphaEvolve
5. System discovers even better algorithms

This isn't speculative. The paper describes it concretely. The versions of Gemini Flash and Pro used in AlphaEvolve are already benefiting from optimizations discovered by earlier versions of AlphaEvolve. The system is already in this self-improvement loop, with no obvious stopping point. It's happening now at Google DeepMind.

Figure 3: The self-accelerating cycle where AlphaEvolve improves its own training infrastructure.

Three Categories of AI-for-Mathematics Systems

AlphaEvolve occupies a distinct niche in the emerging ecosystem of AI systems for mathematical research. Understanding how it differs from related approaches clarifies what it's good at.

Synthesizers (ChatGPT, Claude) Standard LLMs function as knowledge synthesizers. They recombine patterns from training data to generate plausible text. For mathematical questions, they can explain concepts, suggest approaches, even generate code. But they operate by predicting likely text tokens, not by discovering novel solutions. A standard LLM cannot solve a genuinely open problem because the answer doesn't exist in its training data.

Provers (AlphaProof, AlphaGeometry) These systems operate in formal logic systems like Lean. AlphaProof solved two IMO problems by translating them to formal statements and proving them through rigorous logical deduction. These systems excel at verification: proving that a proposed solution is correct. They excel when the proof structure is well-understood but the specific verification is tedious. The limitation: they don't construct new objects or algorithms; they verify logical statements.

Constructors (AlphaEvolve, FunSearch) AlphaEvolve constructs and discovers new algorithms, configurations, and mathematical structures. It doesn't prove statements about existing structures; it builds structures with optimal properties. The 48-multiplication algorithm didn't exist before AlphaEvolve found it. You couldn't prove it correct against existing knowledge because it was unknown.

These three categories address different mathematical problems. Proving a theorem requires a Prover. Understanding a concept requires a Synthesizer. Discovering a new algorithm requires a Constructor. AlphaEvolve is the first system at scale to fill the Constructor role, and you might use all three in sequence: FunSearch or AlphaEvolve to discover an algorithm, AlphaProof to verify its correctness formally, and ChatGPT to explain it to colleagues.

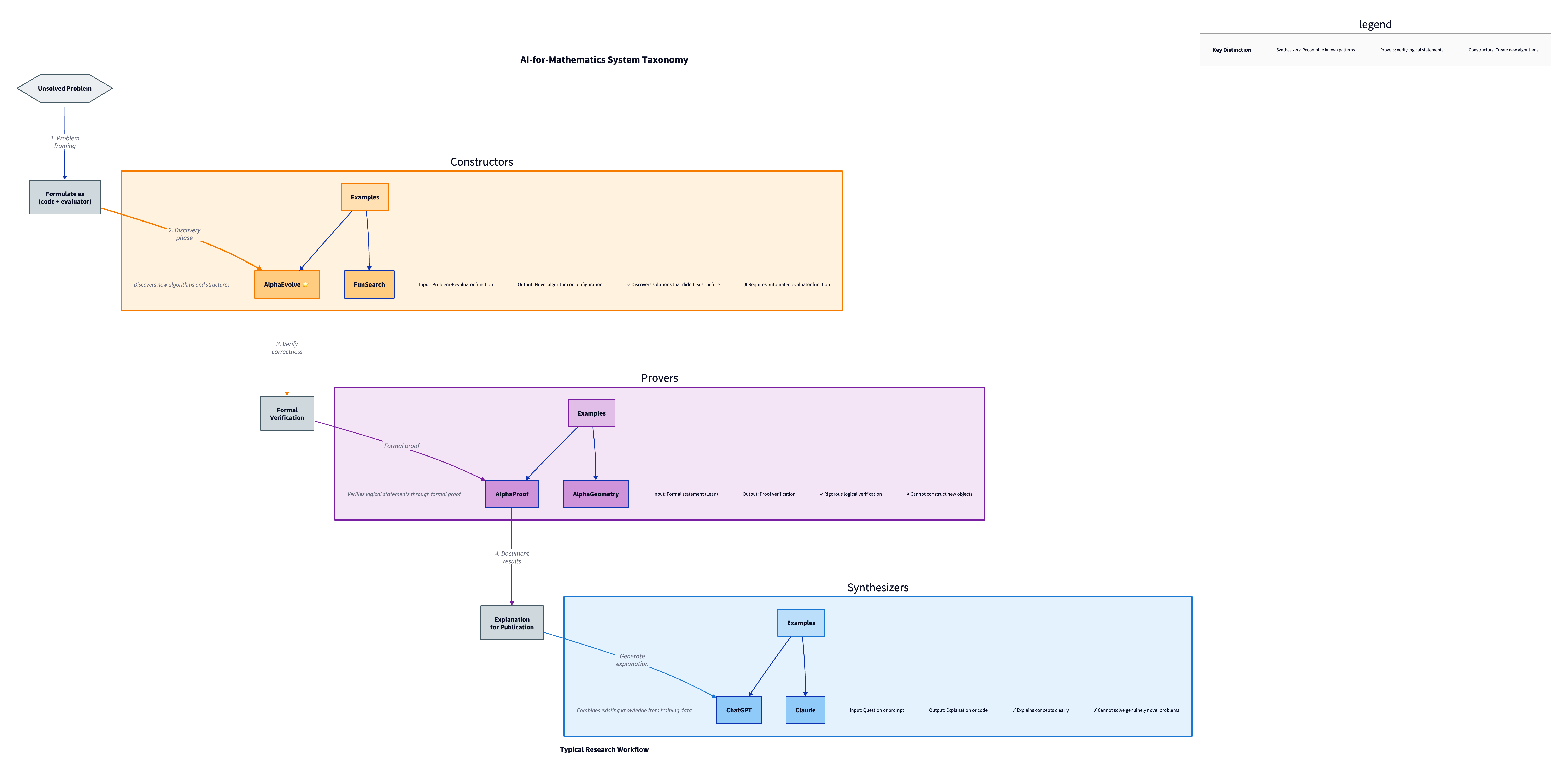Figure 4: Three distinct categories of AI-for-Mathematics systems and their capabilities.

What AlphaEvolve Cannot Do (Yet)

The framework's power comes from its reliance on automated evaluation. This is also its constraint. AlphaEvolve can only solve problems where an automated evaluator function can be written, a function that takes a proposed solution, executes it, and returns a scalar score.

Problem 1: Abstract Judgment Some mathematical questions require qualitative assessment. "Is this proof elegant?" or "Does this theorem unify two seemingly separate fields?" These are meaningful research questions, but they can't be reduced to scalar evaluations the system can automate. AlphaEvolve cannot answer these.

Problem 2: Discovering Conjectures AlphaEvolve can solve problems framed as "find X that optimizes Y." It struggles with "what is an interesting conjecture about X?" Conjecture generation requires intuition about mathematical significance, which isn't easily mechanizable.

Problem 3: Computational Tractability Even with efficient search, some problems are computationally intractable. The paper notes that while 4×4 matrix multiplication was solved, attempting 5×5 matrices would "often run out of memory" (Tao commentary). The search space grows exponentially; computational limits are binding.

Problem 4: Evaluator Design Vulnerability AlphaEvolve can exploit weaknesses in the evaluator. If the evaluator function is poorly designed, the LLM will find edge cases where the evaluator gives high scores for wrong reasons. As Tao notes, the system is "extremely good at locating exploits in verification code." This places a heavy burden on the human designing the evaluator.

Problem 5: Limited Effectiveness on Some Domains The paper acknowledges limited effectiveness on analytic number theory problems (source: paper discussion). Some mathematical domains appear resistant to this approach, possibly because solutions require deep structural insights that aren't easily encoded in code.

These constraints define the framework's appropriate scope: well-defined optimization problems where solutions can be automatically verified. This covers a substantial portion of algorithmic research, but not all mathematics.

Paradigm Shift: From Problem-Solver to Problem-Framer

The deeper implication of AlphaEvolve is a role inversion for human researchers. Terence Tao articulates it directly: "They turned math problems into problems for coding agents."

For centuries, mathematics was primarily a human domain. Mathematicians formulated problems, searched solution spaces (mentally or on paper), and published discoveries. AI tools were seen as assistants, checking computations or verifying claims.

AlphaEvolve inverts this hierarchy. The system becomes the search engine. Humans become problem architects.

Specifically, the researcher must:

1. Define the problem algorithmically (what code structure might solve this?)
2. Design the evaluator (how do we automatically score solutions?)
3. Interpret the results (why is this discovered algorithm interesting?)

The execution, the computational search through program space, is fully automated. The paper notes that researchers could "set up most experiments in a matter of hours" (source: paper methodology). This low setup cost combined with a 95% match-or-beat rate creates a fundamentally new approach to research.

Consider the implications: researchers in fields beyond computer science (biology, physics, chemistry, materials science) might now reframe their unsolved problems as (code + evaluator) tuples. The next breakthrough in materials science might come not from a PhD spending 5 years on a specific approach, but from a researcher writing a 100-line evaluator function and running AlphaEvolve overnight.

This paper will likely trigger what might be called a "gold rush" for computable problems. Researchers across mathematics, physics, biology, and materials science will race to reframe their open problems into this (code + evaluator) format. The next major breakthroughs may come not from using AlphaEvolve, but from cleverly reframing previously intractable problems in ways that fit the framework.

The challenge: problem formulation becomes the bottleneck. How do you translate fuzzy mathematical intuition into a computable evaluator? How do you encode domain-specific constraints that aren't naturally algorithmic? How do you avoid "teaching" the system to exploit loopholes in the evaluator rather than genuinely solving the problem? These become the intellectual challenges.

Technical Foundations: Why Now?

AlphaEvolve isn't conceptually novel. Evolutionary algorithms and genetic programming are decades old. What changed?

Semantic Mutation Through LLMs: Modern LLMs, trained on billions of lines of code, can perform intelligent mutations in concept space, not just random perturbations. They understand that "replace this loop with a NumPy operation" is a meaningful modification even if it changes many tokens.

Large Context Windows: Current LLMs can maintain millions of tokens of context. This enables rich prompts: the parent program, performance feedback, multiple inspiration programs, and detailed descriptions. The LLM has everything needed for intelligent reasoning.

Computational Scale: Running thousands of LLM inferences (each program generation) requires scale. But with modern GPU infrastructure and efficient inference (Gemini Flash achieves 4 million tokens/minute), this is now tractable. A 2015 version of this system would have been computationally infeasible.

Efficient Evaluators: For many mathematical problems, verification is cheap. Once you have an algorithm, checking correctness is tractable. This creates a tight feedback loop.

The combination of these factors (semantic understanding via LLMs, large context windows, computational scale, and efficient evaluation) makes AlphaEvolve viable now, in 2025, when it wouldn't have been viable earlier. The three-year trajectory matters: FunSearch (2023) demonstrated that LLM-guided genetic algorithms could discover novel single functions. AlphaEvolve (2025) generalizes this to full programs across hundreds of lines and multiple components.

Why This Matters for Engineering

For senior engineers and researchers, AlphaEvolve represents three key insights:

1. Algorithmic Problems Are Solvable at Scale For decades, certain algorithmic problems seemed "stuck." Strassen's record stood because the search space was deemed intractable. AlphaEvolve demonstrates that with the right search strategy (guided by semantic understanding) and sufficient computational resources, even highly constrained algorithmic problems yield to systematic exploration. How many other "solved" problems with tight records might also be improvable?

2. Automated Verification is the Key Constraint The limiting factor isn't the discovery process; it's defining what "better" means. Problems with clear, automatable metrics (faster code, more spheres packed, higher inapproximability bounds) are solvable. Problems requiring human judgment aren't. This suggests that clarity of specification is increasingly valuable in research.

3. Human Creativity Shifts to Problem Formulation As systems like AlphaEvolve automate algorithm discovery, human expertise becomes most valuable in problem formulation. The researchers who excel at this new era will be those who can identify interesting problems, specify them precisely, and design evaluators that capture what matters. The execution becomes commoditized.

4. The Economics Have Shifted What would have required years of PhD research now potentially requires hours of setup plus overnight computation. The cost-benefit calculation for attacking hard problems has fundamentally changed. Within a decade, not applying AlphaEvolve-like approaches to algorithmic problems may seem as absurd as not using GPUs for numerical computing.

5. Watch the Feedback Loops Systems that discover optimizations for their own underpinnings (like AlphaEvolve optimizing FlashAttention) create self-accelerating cycles. These compound effects matter. Look for these in your domain.

Open Questions and Future Directions

Several questions remain unanswered:

Generalization: Can algorithms discovered for one problem generalize to similar problems? If AlphaEvolve discovers a matrix multiplication algorithm for 4×4 matrices, does that insight transfer to 5×5 matrices?

Formal Verification Integration: Could systems like AlphaEvolve be combined with formal theorem provers to automatically generate and verify correctness proofs?

Transfer Learning: If you run AlphaEvolve on 67 problems sequentially, does the experience from early problems improve performance on later ones?

Evaluator Design: What makes a good evaluator? What are common pitfalls? How much does AlphaEvolve performance vary based on evaluator quality?

Human-AI Collaboration: What role remains for human mathematicians? Can they guide the search by providing insights about problem structure?

The 80-page arXiv paper provides detail on these questions, but they remain open research directions. The field is at an early stage where the discovery process itself is being discovered. How many open conjectures could be tackled if reframed correctly? The research community is about to find out.

Conclusion: The Next Frontier

AlphaEvolve breaks Strassen's 56-year record not through brute-force search but through intelligent exploration guided by semantic understanding of algorithms. More importantly, it demonstrates that this approach generalizes. The same system that discovered a matrix multiplication optimization also improved data center scheduling, accelerated AI training, and solved decades-old geometry problems.

The implications extend beyond any single discovery. AlphaEvolve represents a shift in how algorithmic research is conducted. Rather than humans directly searching for solutions, we frame problems precisely and let automated systems explore the solution space. This doesn't replace human mathematicians and engineers; it amplifies them. The researchers who excel will be those who can identify interesting problems, specify them clearly, and interpret the discovered solutions.

The most remarkable aspect might be the self-acceleration loop. Algorithms it discovers improve the LLMs that power it, which improve the algorithms it discovers next. We're entering an era of machine-aided scientific discovery, where the tools amplify themselves. The 48-multiplication algorithm is proof of concept. The real breakthroughs will come as researchers across domains learn to frame their hardest problems in this framework. That transformation in how research is conducted, more than any single discovery, is what makes this work landmark.